수 학 (6면 중
2 면)
◦ 문제지 전체 면수가 맞는지 확인하시오.
◦ 모든 문항에는 배점이 표시되어 있습니다.
1. 다음은 수학교육론 강의 시간에 다양한 현상과 결부된 개념을
학습한 다음, 이를 요약한 것이다. (가)와 (나)의 설명에 해당하는
개념을 순서대로 쓰시오. [2점]
(가)
◦현실에 질서를 부여하는 활동으로, 현상이 본질로 조직
되고 그 본질이 다시 현상이 되는 끊임없는 재조직화의
과정임.
◦현실의 여러 현상들을 수학적인 수단을 사용하여 조직
하고 현상들 사이에서 그 정리수단인 본질을 찾는 활동임.
◦트레퍼스(A. Treffers)는 이 활동이 주어진 상황마다
다르며 다양한 활동으로 세분화될 수 있다고 함.
(나)
◦비수학적 문제 상황에서 출발한다는 면에서 문제
해결과는 차별화됨.
◦다음과 같은 일련의 과정을 거침.
① 실세계 현상을 관찰하여 그 현상 속에 내재된
문제를 명확히 구성함.
② 구성된 문제를 해석하여 현상에 적합한 모델을
구축함.
③ 모델 내에서 적절한 수학적 분석을 실시함.
④ 분석 결과를 얻고 현상에 맞도록 그 결과를
재해석하여 결론을 도출함.
2. 군 준동형사상(group homomorphism)
× → 를
로 정의하자. 의 핵(kernel)을 라 할 때,
잉여군(상군, factor group, quotient group) × 의
위수(order)를 구하시오. (단, 양의 정수 에 대하여 은 위수가
인 덧셈 순환군(additive cyclic group)이다.) [2점]
3. 이차함수
과 양의 정수 에 대하여 을
특이적분(이상적분, improper integral)
∞
의 수렴
또는 발산에 따라 다음과 같이 정의하자.
∞
∞
가 수렴
∞
가 발산
∞
의 값을 구하시오. [2점]
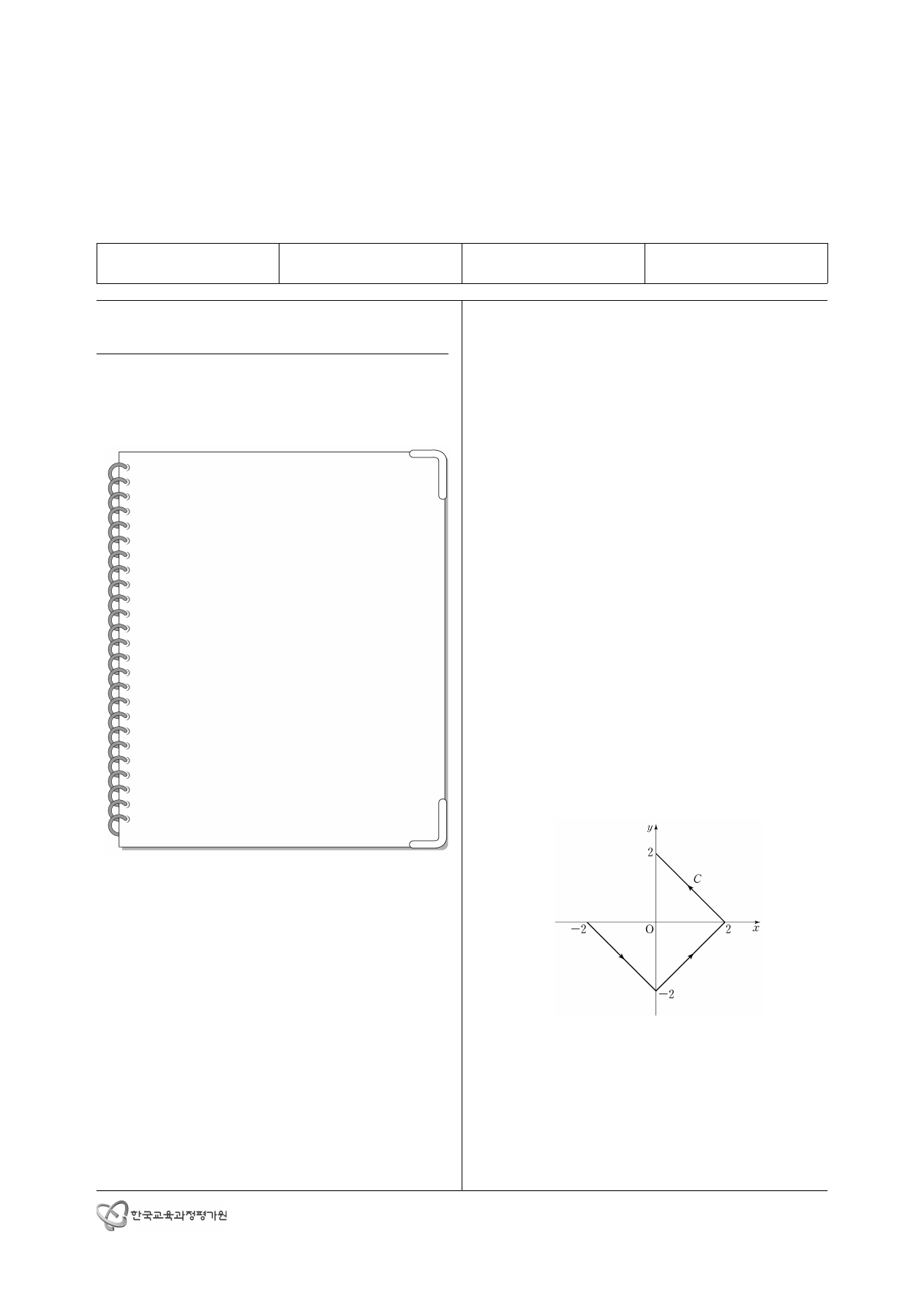
4. 그림과 같이 좌표평면에서 곡선 는 점 에서 시작하여
점 와 점 을 지나 점 까지 선분으로 연결한
경로이다.
의 값을 구하시오. [2점]
2016학년도 중등학교교사 임용후보자 선정경쟁시험
수 학
수험 번호 : (
)
성 명 : (
)
제1차 시험
2 교시 전공 A
14문항 40점
시험 시간 90분

수 학 (6면 중
3 면)
5. 좌표평면에서 영역 가
∈ ≤ ≤ ≤ ≤
일 때, 함수 → 를 다음과 같이 정의하자.
≥ sin
sin
sin
두 반복적분의 합
sin
sin
의 값을 구하시오. [2점]
6. 차원 유클리드 공간
에서 단위속력곡선(unit speed curve)
→
의 점 에서의 곡률(curvature) 는
이다. 곡선 → 을
′
로 정의할 때, 에서 까지 곡선 의 길이를 구하시오.
[2점]
7. 앞면이 나올 확률이 인 동전을 학생 A가 번
던지고, 학생 B가 번 던진다. 학생 A가 던져서 앞면이 나온
횟수와 학생 B가 던져서 앞면이 나온 횟수의 합이 일 때,
학생 A가 던져서 앞면이 나온 횟수가 일 확률이
이다.
의 값을 구하시오. [2점]
8. 두 연속확률변수 , 가 서로 독립이고,
확률밀도함수(probability density function)가 각각
이다. 확률변수 의 확률밀도함수 를 구하시오.
[2점]
수 학 (6면 중
4 면)
9. 다음은 역사 발생적 원리에 대한 설명과 예비 교사가 작성한
수업 계획서의 일부이다.
(가) 역사 발생적 원리
수학이 발생된 것으로 파악하고 학습자가 학습 과정에서
수학의 발생을 경험하게 하는 원리이다. 이 원리는 클레로
(A. Clairaut), 클라인(F. Klein), 퇴플리츠(O. Toeplitz) 등이
주장하였다.
(나) 수업 계획서
◦단원 제목 : 삼각함수
◦지도 순서
1단계
⇨
2단계
⇨
3단계
⇨
4단계
함수
정의하기
표로
나타내기
그래프로
그리기
현실에
응용하기
- 단계에서는 함수 sin를 정의한다.
- 단계에서는 함수 sin에서 와 사이의 관계를 표로
나타낸다.
- 단계에서는 단계에서 작성한 표를 바탕으로 그래프를
그린다.
- 단계에서는 함수 sin와 관련된 응용문제를 다룬다.
역사 발생적 원리에 따라 수학 수업을 진행할 때, 수학 교수․학습
에서의 의의를 가지 쓰시오. 또한 이 원리에 기초하여 (나)에서
제시한 지도 순서를 재구성하고, 그 이유를 지도 내용과 관련지어
설명하시오. [4점]
10. 다음은 수학 교사를 위한 ‘평가’ 연수 시간에 이루어진 대화의
일부이다.
김 강사 : 서술형 평가의 중요성에 대해 말씀을 드렸습니다. 혹시
질문이 있으세요?
박 교사 : 서술형 평가는 선택형 평가와 비교해 장점도 있지만,
채점의 어려움이 걱정입니다.
김 강사 : ‘총체적 점수화 방법’을 적용하여 채점하면 좋을 듯
합니다. <자료 1>로 설명해 볼게요.
<자료 1>
(선택형)
가 정수가 되는
이하의 모든 양의 정수 의 합은?
① ② ③ ④ ⑤
정답률
(%)
답지반응률(%)
① ② ③ ④ ⑤
(서술형)
가 정수가 되는 이하의 모든 양의 정수 의
합을 풀이 과정과 함께 쓰시오. [10점]
… (중략) …
박 교사 : 아, 풀이 전반에 걸쳐 하나의 점수를 부여하는 방법
이군요. 다른 채점 방법도 있나요?
김 강사 : 네, ‘분석적 점수화 방법’이 있습니다. 문제를 해결
하는 데 필요한 내용이나 과정을 몇 단계로 구분하여
단계별로 점수를 부여하는 방법입니다.
<자료 2>는 <자료 1>의 (서술형) 문제에 대해 어느
교사가 작성한 채점 기준표와 학생 A의 답안입니다.
<자료 2>
채점 기준표
채점 영역
채점 요소
배점
문제 이해 제곱근의 성질
( ≥ )을 이해함
문제해결
를
× × 또는
로 고침
× × 또는
를 이용하여 만족
하는 수를 모두 구함
답 구하기
만족하는 모든 수의 합을 구함
학생 A의 답안
( ≥ )
이므로
가 정수가 되기 위해서는
이고, 또한
× ×
이므로
가 정수가 되기 위해서는 이다.
따라서 만족하는 모든 양의 정수의 합은 이다.
… (중략) …
박 교사 : 네, 서술형 평가 실시에 큰 도움이 될 것 같습니다.
교사의 수업 개선에 초점을 맞추어 서술형 평가의 장점을 <자료 1>,
<자료 2>와 관련지어 서술하시오. 또한 <자료 2>의 채점 기준표에
근거하여 ‘학생 A의 답안’을 채점한 점수를 쓰고, 그 점수를
부여한 이유를 설명하시오. [4점]

수 학 (6면 중
5 면)
11. 함수 ∞→ 가 구간 ∞ 에서 미분가능하다.
모든 점 ∈ ∞ 에 대하여 ′ ≤ 이고 일 때,
≤
임을 보이시오. 또한 ≤ 이면 방정식
는 단 하나의 해를 가짐을 보이시오. (단, 은 상수이다.)
[4점]
12. 실수 전체의 집합 에서 ∈ 를 기저(base,
basis)로 하는 위상을 ℑ 이라 하고, ∈ 를
기저로 하는 위상을 ℑ 라 하자. 적공간(곱공간, product space)
ℑ
× ℑ 에서 집합
∈× ≤
의 내부(interior)
o 를 풀이 과정과 함께 쓰시오. 또한
의 폐포(closure)
와 의 경계(boundary) 를 구하시오.
(단, ∈ ≤ , ∈ ≤
이다.) [4점]

수 학 (6면 중
6 면)
13. 정수 은 법(modulo) 에 대한 원시근(primitive root)이고,
는 소수이다. 정수
에 대하여 ≡ mod 를 만족
하는 가장 작은 양의 정수 의 값을 풀이 과정과 함께 쓰시오.
[4점]
14. 유리수 체 위에서 대수적인 원소 와 단순확대체(simple
extension field) 가 있다. 가 의 부분체이고
irr
⋯
⋯ ∈
일 때, ⋯ 임을 보이시오.
또한
이고
일 때, irr 를 구하시오.
(단,
이고, irr 는 위에서 의 기약다항식
(최소다항식, irreducible polynomial, minimal polynomial)이다.)
[4점]
<수고하셨습니다.>