
일반물리
General Physics
7 장 회전운동과 중력의 법칙
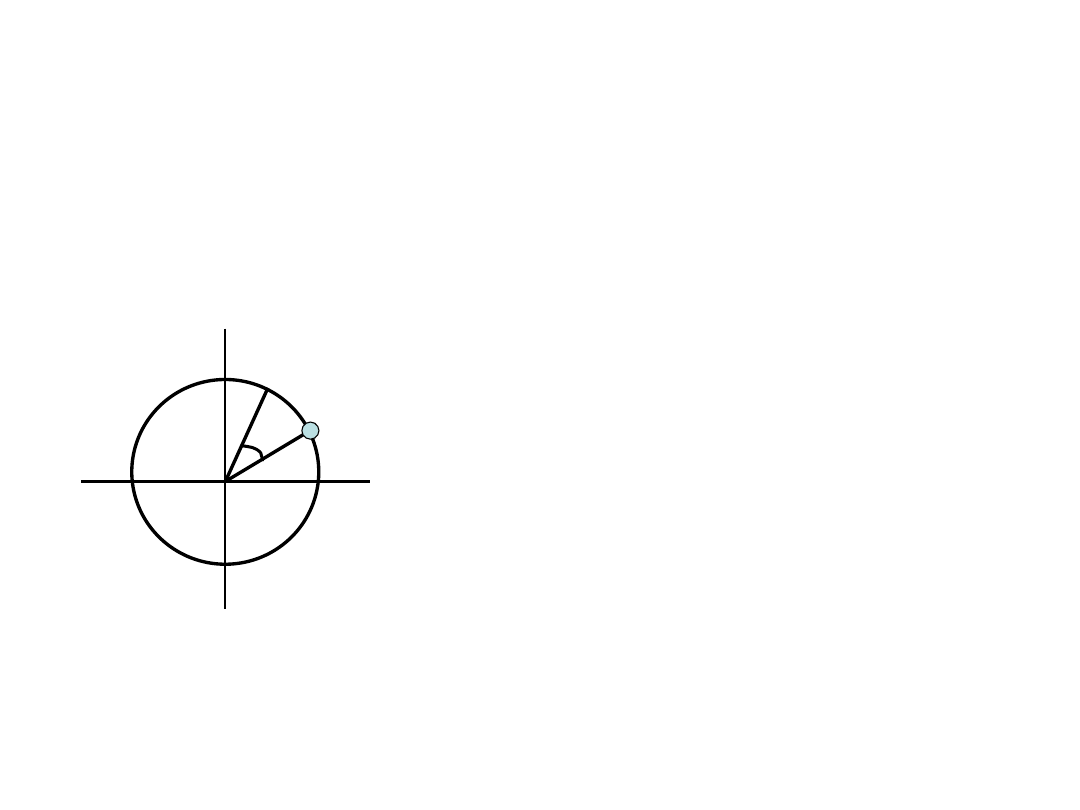
7.1 각 속력과 각 가속도
원운동을 편리하게 기술하기 위해서 “라디안” 단위를 도입한다. 1
라디안 = 1 radian = 360o/2 = 360o/(2×3.14159) = 57.3o
1
회전= 360o 회전 = 2 radian
r
S
S = r각각각각각각각각
평균 각속도, = / t
각속도 = lim / t = d / dt
t 0
각속도 단위; rad/s

헬리콥터 날개가 320 rev/min의 각 속력으로 회전을 한다. 이
속력을 rad/s 로 나타내라.
1 rev/min
는 1 revolution/minute 의 뜻으로 분당 1 회전을 한다는
의미로 1rpm( 1 revolution per minute)으로 표기하기도 한다.
1
초 회전 수 = 320 rev/min = 5.33 rev/s
각속도
= 5.33 ×
2 rad/s = 10.7 rad/s

각 가속도 단위;
각 가속도

• 등 각 가속도란; 가속도가 시간에 대해서 크기와 방향이 일정함
상수임 (
예; 등가속도 운동)
= d / dt d = dt
t
ddt
t) dt
0
t
d
o
7.2
등 각 가속도를 가진 회전 운동
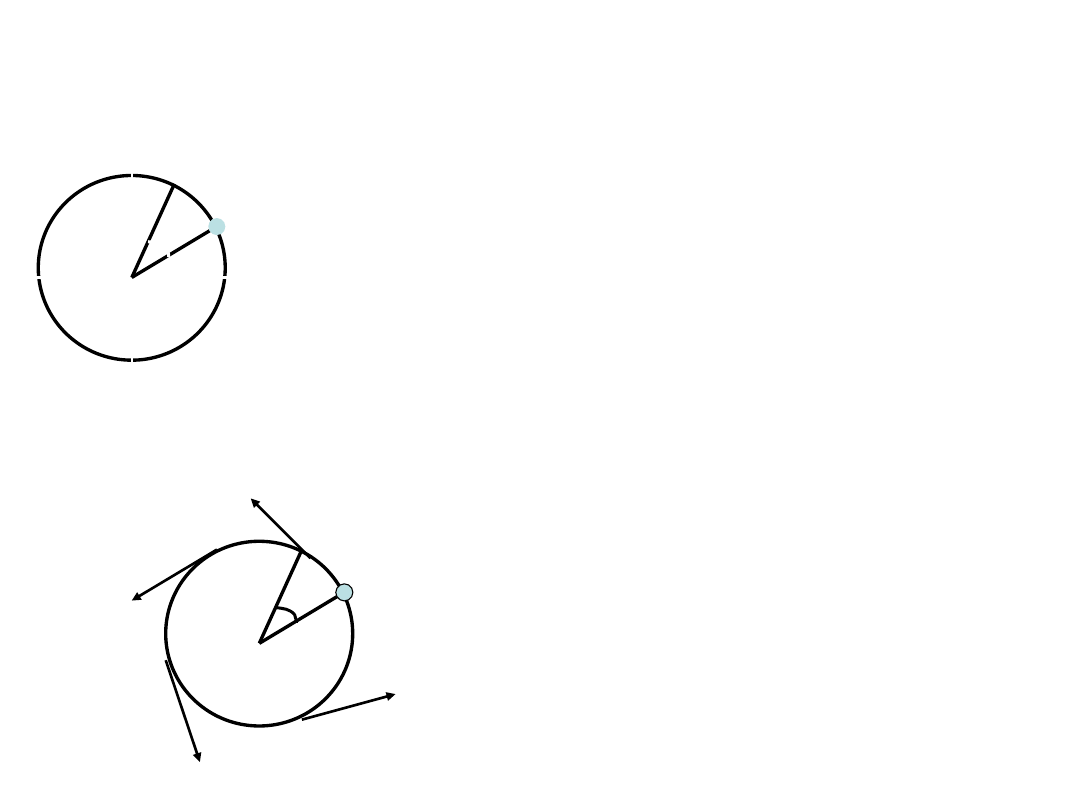
7.3
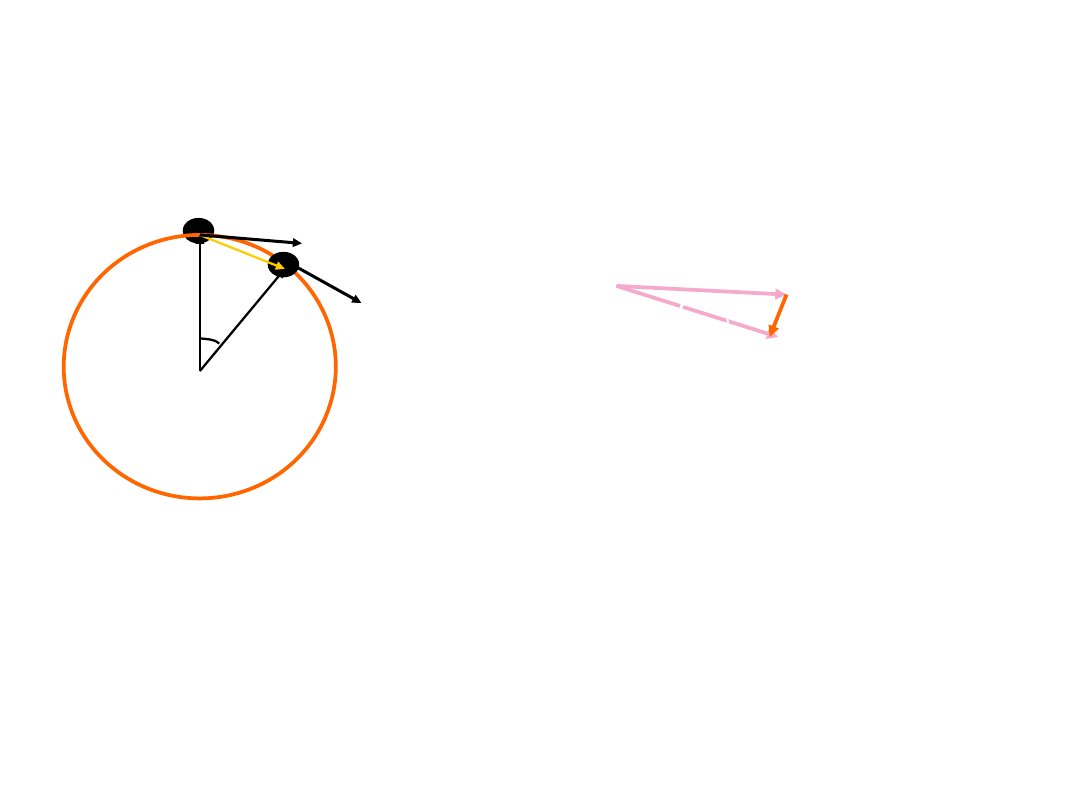
각운동과 선운동 물리량과의 관계
r
s = vt
s = r s / r
선 속도
v 는 원주의 접선방향
r
s = vt
v
v
v
v

회전운동과 선형운동과의 비교
각가속도 가 일정한
회전운동
가속도 a 가 일정한
선형운동
t
v = v
0 + a t
t½
t
x = x
0 + v0 t + ½ a t
2
v2 – v
0
2
= 2a S
변수
변수 x, v
예) 자전거 바퀴가 각 가속도 3.5 rad/s로 회전한다. t
0 =0 일때 초기 각
속력이 2 rad/s 이다. (a) 2초 동안 회전한 각도와 (b) 2초 일때 각 속력을
구하시오.

예) 컴펙트 디스크는 읽기 헤드가 디스크의 중심으로부터 바깥쪽으로
움직이며 헤드 위치에서 선 속력이 항상 1.3 m/s 의 일정한 값을 유지한다.
중심으로부터 5 cm, 8 cm일때 디스크의 각 속력을 구하시오
예) 레코드 판은 일정한 속력으로 회전한다. 회전수가 45 rev/min 인 경우
중심에서 5 cm, 8 cm 인 곳의 선속력을 구하시오
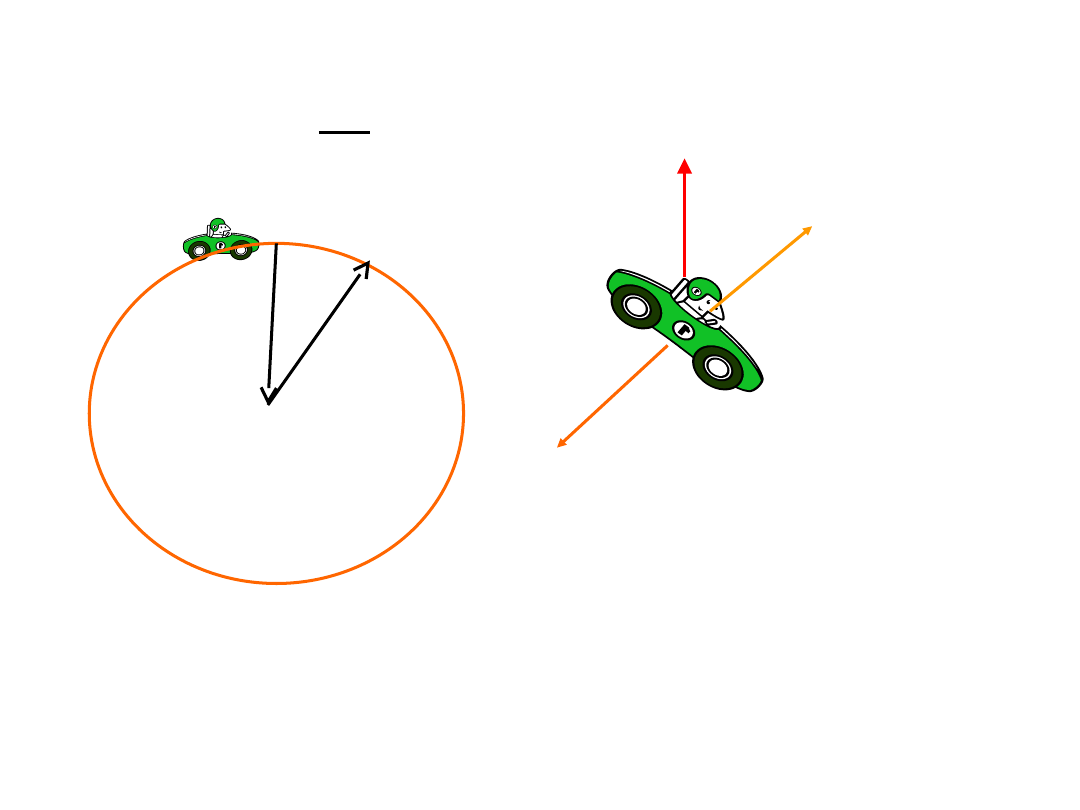
7.4
구심가속도
원운동의 근원은 원운동의 중심으로 향하는
구심력
s
r
v
v
v
v
v

구심가속도
a = a
C = v
2
/r = r2
회전운동의 근원은 원운동의 중심으로 향하
구심력
s
r
v
v
v
v
v
a
C
예) 시험용 자동차가 반지름 50 m 인 트랙을 10 m/s 의 일정한 속속력으로
돌고 있다. (a)구심가속도와 (b) 각속력을 구하시오.
구심력 F = m a
C = m r
v 2
a
C
r = 50 m
반경 50 m, 속도 13.4 m/s 인 경우에 미끄러지지 않고 회전하기
위한 정지마찰계수를 구하시오.
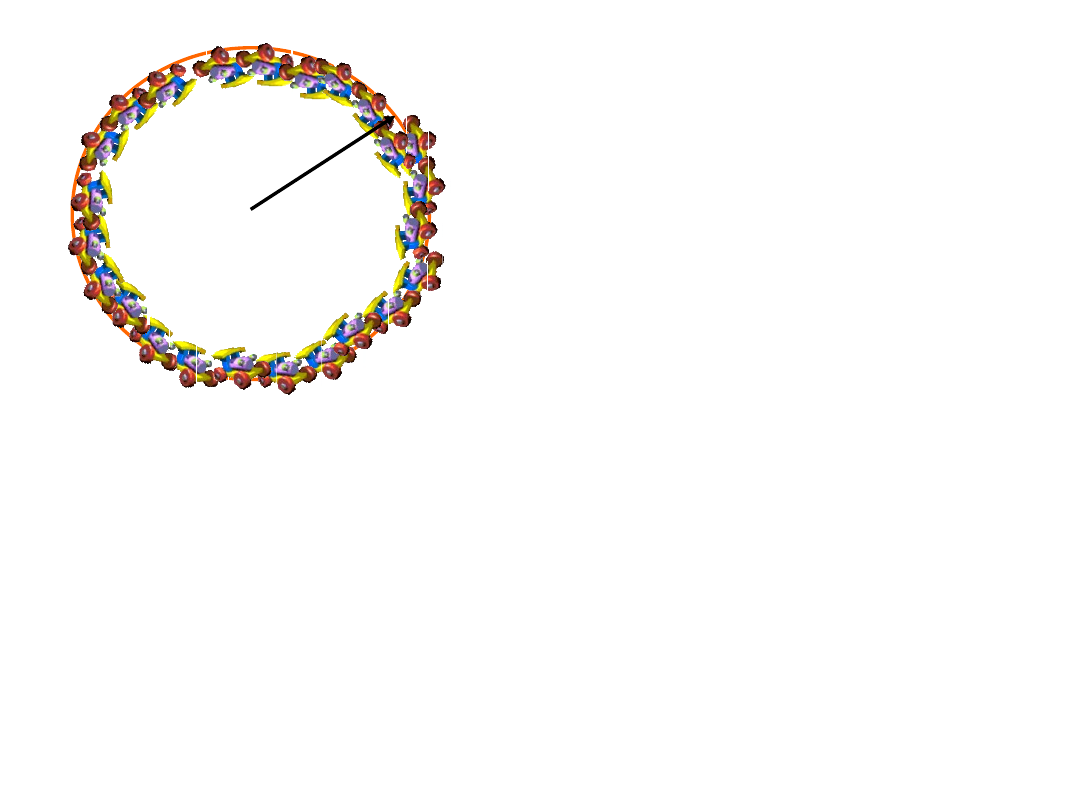
R
최고점에서 최소한의 속도를 구하시오
중력이 원심력을 제공
바닥에서의 속도를 구하시오

There is a popular story that Newton was
sitting under an apple tree, an apple fell
on his head, and he suddenly thought of
the Universal Law of Gravitation. As in all
such legends, this is almost certainly not
true in its details, but the story contains
elements of what actually happened.
7.5
뉴턴의 만유인력 법칙
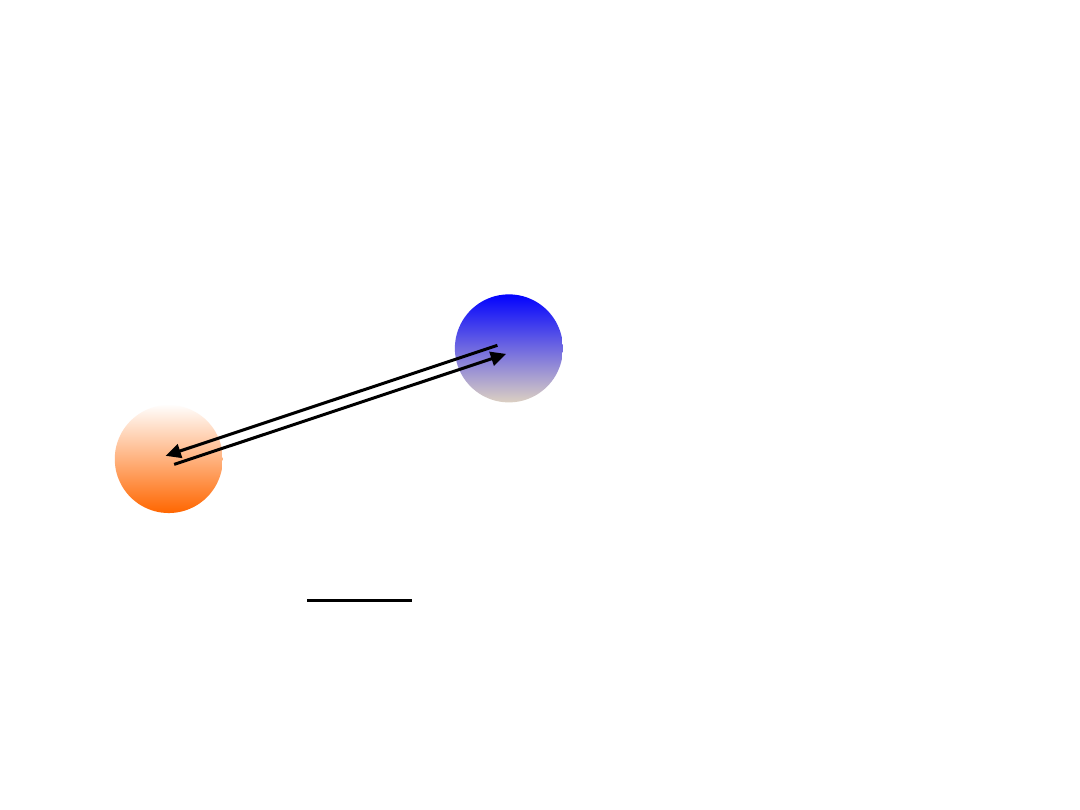
만유인력 법칙;
우주안에 있는 모든 입자는 모든 입자들에게 인력을 작용하고, 이 인력은
입자들의 질량의 곱에 비례하고 그들 사이의 거리의 제곱에 반비례한다.
r
m
1
m
2
∴ F = G
r 2
m
1·m2
G;
중력상수(gravitational constant)
G =

R
E
지구질량; M
E = 5.98 ×10
24
kg
지구반경; R
E = 6.38 ×10
6
m
∴ F =
=
m
M
E
∴ g =
∴ g =
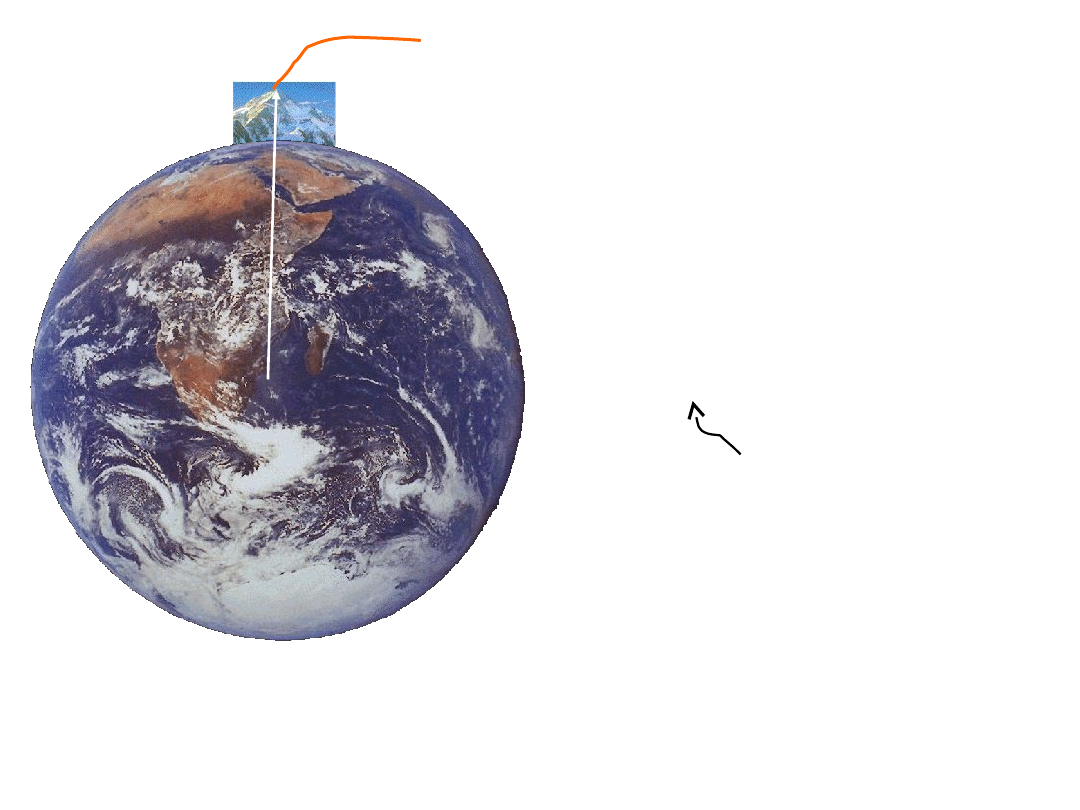
히말라야산 정상
( 해발 약 8800 m )
지구중심에서 히말라야산 정상까지 거리
r
r = R
E + 8800 m = 6388800 m
r
히말라야산 정상에서 중력가속도 g’
은,
g’ = 9.777
m/s2 ≈ 9.8 m/s2
지표에서의 중력가속도 g = 9.8
m/s2 와
큰 차이가 없다.

목원대학교 개교
50주년 기념 로켓 발사
1) 지구 반경의 높이까지 올라가면,
중력가속도의 크기는 얼마인가
;
2R
E
2)
로켓의 질량이 500 kg 이면, 이때의 무게는
얼마인가?
7.6
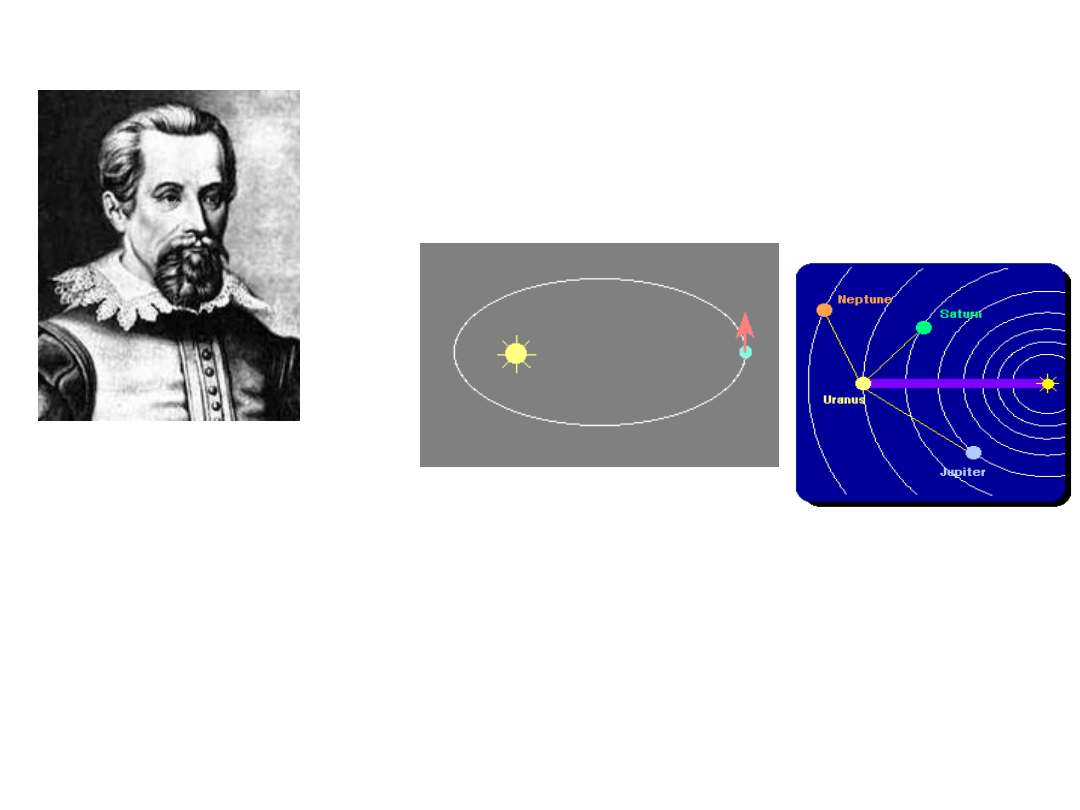
케플러의 법칙
Johannes Kepler
1571 - 1630
제
1 법칙; 모든 행성을 태양을 중심으로 타원
궤도를 따라 운동한다
.
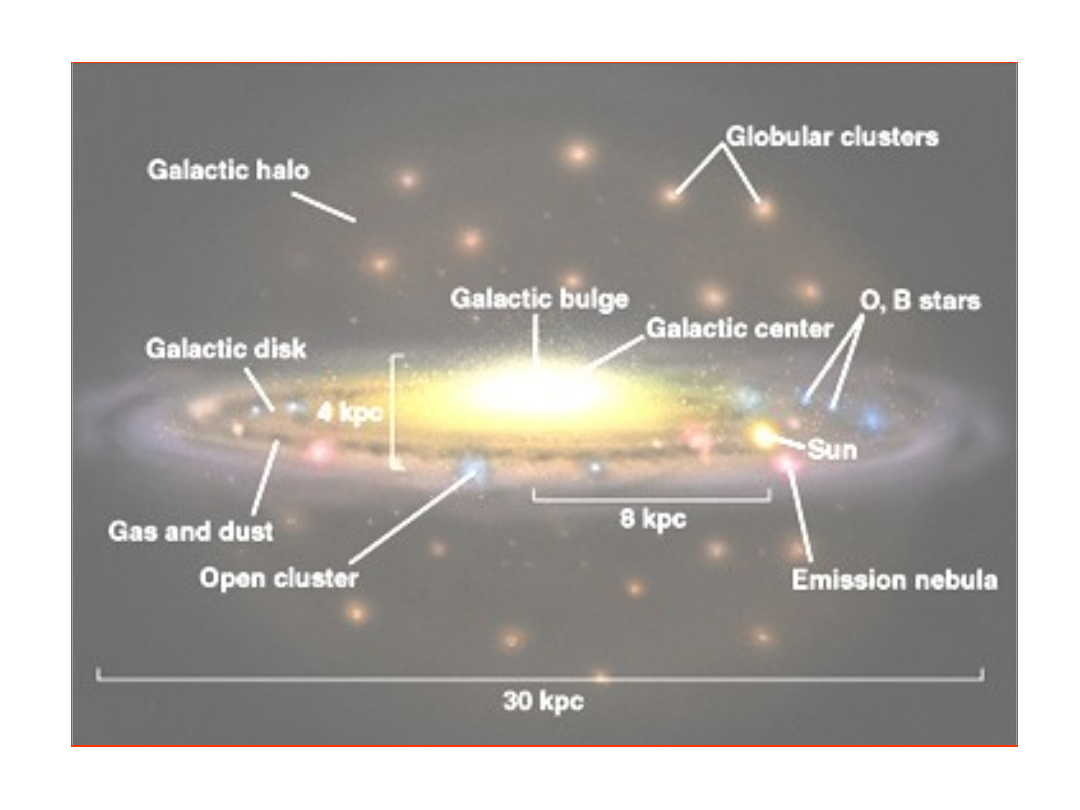
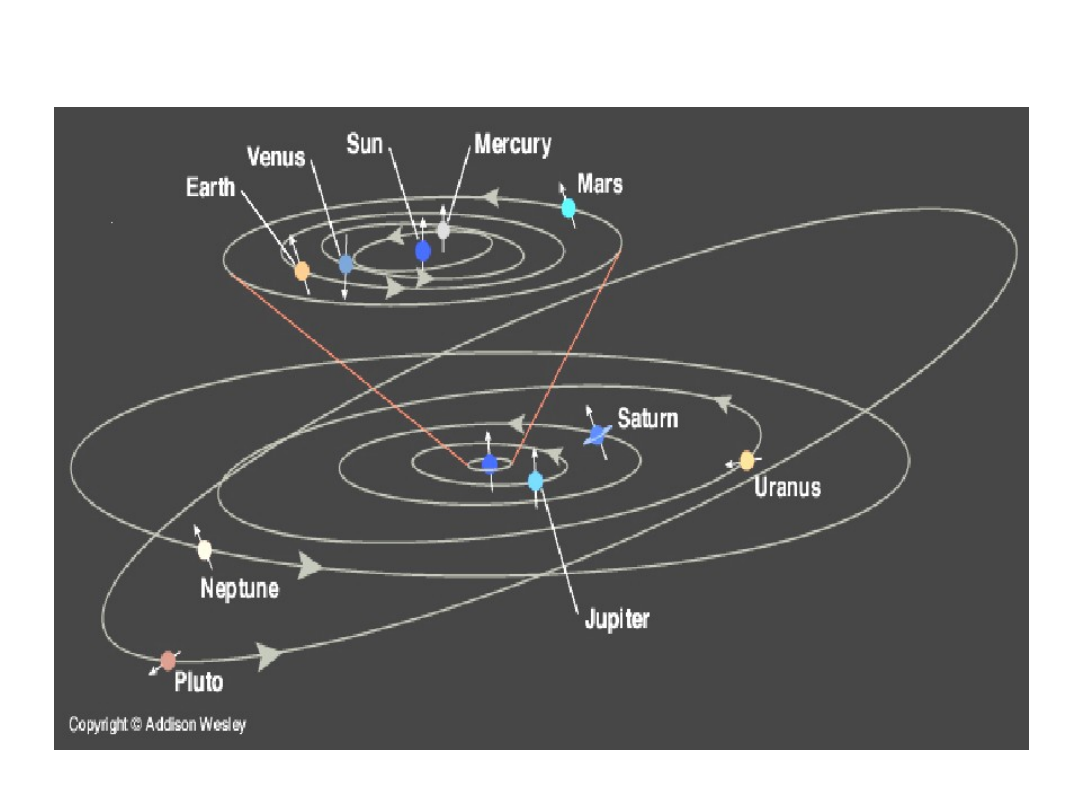
Solar (Star) System
A star and all the material which orbits it, including
its planets and moons
제
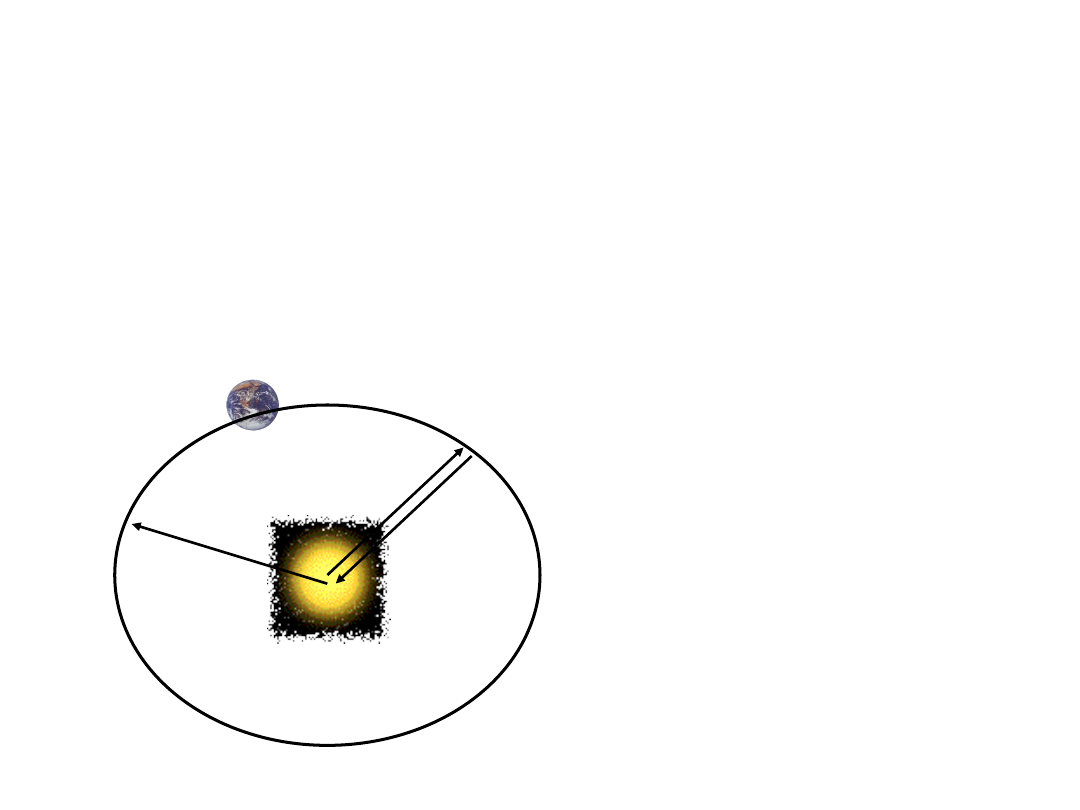
2 법칙; 태양으로부터 행성까지 이은 선은 같은 시간 동안에 같은
면적을 지나게 된다
. 각운동량 보존의 법칙
제
3 법칙; 행성의 궤도 주기의 제곱은 행성으로부터 태양까지
거리의 세제곱에 비례한다
.
운동궤도를 원형이라 생각하고 증명
F
G
F
C
태양의 질량; M
S , 행성의 질량 MP
r
주기 T = 2r / v v = 2r / T
∴ T2 = ( 4 / GM
S) r
3
= K
S r
3
K
S = ( 4
/ GM
S) = 2.97 ×10
-19
s2/m3
r
문제
) 지표로부터 1000 km 지점에서 지구를 돌고 있는 인공위성의
속도와 주기를 구하시오
.