
CHAPTER 2
Measurements and Calculations
1.
measurement
2.
“Scientific notation” means we have to put the decimal point after the first significant figure, and
then express the order of magnitude of the number as a power of ten. So we want to put the
decimal point after the first 2:
2,421 2.421 × 10to some power
To be able to move the decimal point three places to the left in going from 2,421 to 2.421, means
I will need a power of 103 after the number, where the exponent 3 shows that I moved the decimal
point 3 places to the left.
2,421 2.421 × 10to some power = 2.421 × 103
3.
a.
9.651
b.
3.521
c.
9.3241
d.
1.002
4.
a.
106
b.
10–2
c.
10–4
d.
109
5.
a.
positive
b.
positive
c.
negative
d.
negative
6.
a.
negative
b.
zero
c.
negative
d.
positive
7.
a.
The decimal point must be moved one space to the right, so the exponent is negative;
0.5012 = 5.012 × 10–1.
b.
The decimal point must be moved six spaces to the left, so the exponent is positive;
5,012,000 = 5.012 × 106.
3

Chapter 2: Measurements and Calculations
c.
The decimal point must be moved six spaces to the right, so the exponent is negative;
0.000005012 = 5.012 × 10–6.
d.
The decimal point does not have to be moved, so the exponent is zero;
5.012 = 5.012 × 100.
e.
The decimal point must be moved three spaces to the left, so the exponent is positive;
5012 = 5.012 × 103.
f.
The decimal point must be moved three spaces to the right, so the exponent is negative;
0.005012 = 5.012 × 10–3.
8.
a.
The decimal point must be moved three spaces to the right: 2,789
b.
The decimal point must be moved three spaces to the left: 0.002789
c.
The decimal point must be moved seven spaces to the right: 93,000,000
d.
The decimal point must be moved one space to the right: 42.89
e.
The decimal point must be moved 4 spaces to the right: 99,990
f.
The decimal point must be moved 5 spaces to the left: 0.00009999
9.
a.
six spaces to the right
b.
five spaces to the left
c.
one space to the right
d.
The decimal point does not have to be moved.
e.
18 spaces to the right
f.
16 spaces to the left
10.
a.
three spaces to the left
b.
one space to the left
c.
five spaces to the right
d.
one space to the left
e.
two spaces to the right
f.
two spaces to the left
11.
To say that scientific notation is in standard form means that you have a number between 1 and
10, followed by an exponential term.
a.
The decimal point must be moved 4 spaces to the left, so the exponent will be 4:
9.782 × 104
b.
42.14 must first be converted to 4.214 × 101 and then the exponents combined:
4.214 × 104
c.
0.08214 must first be converted to 8.214 × 10–2 and then the exponents combined:
8.214 × 10–5
d.
The decimal point must be moved four spaces to the right, so the exponent will be –4:
3.914 × 10–4
4

Chapter 2: Measurements and Calculations
e.
The decimal point must be moved two spaces to the left, so the exponent will be 2:
9.271 × 102
f.
The exponents must be combined: 4.781 × 10–1
12.
a.
The decimal point must be moved 3 places to the right: 6,244
b.
The decimal point must be moved 2 spaces to the left: 0.09117
c.
The decimal point must be moved 1 space to the right: 82.99
d.
The decimal point must be moved 4 spaces to the left: 0.0001771
e.
The decimal point must be moved 2 spaces to the right: 545.1
f.
The decimal point must be moved 5 spaces to the left: 0.00002934
13.
a.
1/1033 = 9.681 10–4
b.
1/105 = 1 10–5
c.
1/10–7 = 1 107
d.
1/0.0002 = 5 103
e.
1/3,093,000 = 3.233 10–7
f.
1/10–4 = 1 104
g.
1/109 = 1 10–9
h.
1/0.000015 = 6.7 104
14.
a.
1/0.00032 = 3.1 103
b.
103/10–3 = 1 106
c.
103/103 = 1 (1 100); any number divided by itself is unity.
d.
1/55,000 = 1.8 10–5
e.
(105)(104)(10–4)/10–2 = 1 107
f.
43.2/(4.32 10–5) =
1
-5
4.32 10
4.32 10
= 1.00 106
g.
(4.32 10–5)/432 =
-5
2
4.32 10
4.32 10
= 1.00 10–7
h.
1/(105)(10–6) = 1/(10–1) = 1 101
15.
mass, kilogram; length, meter; temperature, kelvin
16.
a.
kilo
b.
milli
c.
nano
d.
mega
5

Chapter 2: Measurements and Calculations
e.
deci
f.
micro
17.
Since a meter is longer than a yard, the floor will require somewhat more than 25 square yards of
linoleum. 25 m2 = 5 m × 5 m = 5.47 yd × 5.47 yd = 30 yd2
18.
Since a pound is 453.6 grams, the 125-g can will be slightly more than ¼ pound.
19.
Since a liter is slightly more than a quart, and since 4 quarts make 1 gallon, 48 liters will be
approximately 12 gallons.
20.
Since 1 inch = 2.54 cm, the nail is approximately an inch long.
21.
100 km ×
1 mi
1.6093 km
= 62 km
22.
23.
2 m ×
100 cm
1 m
= 200 cm;
24.
1.62 m is approximately 5 ft, 4 in. The woman is slightly taller.
25.
a.
kilometers
b.
meters
c.
centimeters
d.
micrometers
26.
a.
inch
b.
yard
c.
mile
27.
a.
about 4 liters
b.
about half a liter (500 mL)
c.
about 1/4 of a liter (250 mL)
28.
b (the other units would give very small numbers for the length)
29.
We estimate measurements between the smallest divisions on the scale; since this is our best
estimate, the last significant digit recorded is uncertain.
30.
When we use a measuring device with an analog scale, we estimate the reading to 0.1 of the
smallest scale divisions on the measuring scale. Since this last reading is decided by the user, not
by the divisions on the measuring scale, the final digit of the measurement is uncertain no matter
how careful we may be in making the determination.
6

Chapter 2: Measurements and Calculations
31.
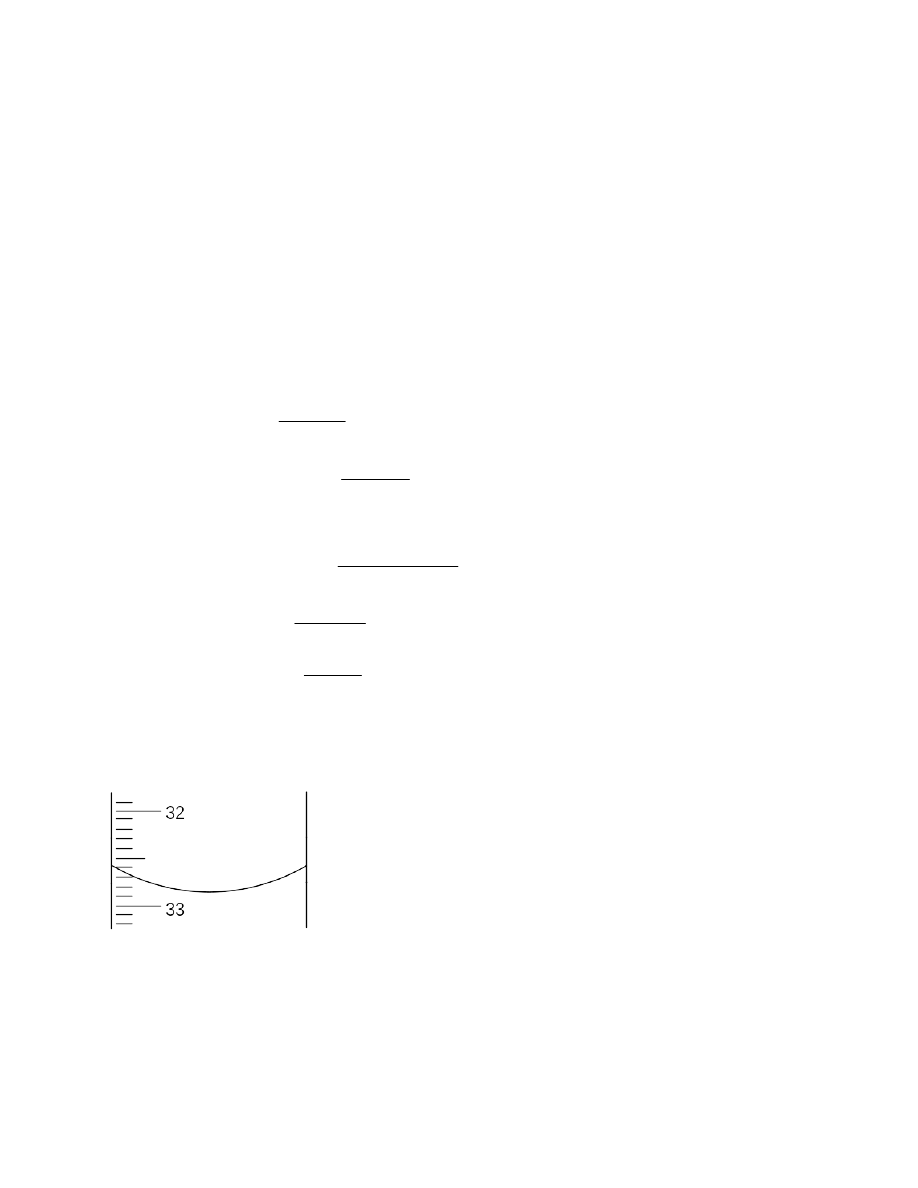
The third figure in the length of the pin is uncertain because the measuring scale of the ruler has
tenths as the smallest marked scale division. The length of the pin is given as 2.85 cm (rather than
any other number) to indicate that the point of the pin appears to the observer to be half way
between the smallest marked scale divisions.
32.
The scale of the ruler shown is only marked to the nearest tenth of a centimeter; writing 2.850
would imply that the scale was marked to the nearest hundredth of a centimeter (and that the zero
in the thousandths place had been estimated).
33.
a.
three
b.
two
c.
two
d.
four
34.
a.
probably only two
b.
infinite (definition)
c.
infinite (definition)
d.
probably one
e.
three (the race is defined to be 500. miles)
35.
increase the preceding digit by 1
36.
It is better to round off only the final answer, and to carry through extra digits in intermediate
calculations. If there are enough steps to the calculation, rounding off in each step may lead to a
cumulative error in the final answer.
37.
a.
2.55 × 105
b.
2.56 × 10–4
c.
4.79 × 104
d.
8.21 × 103
38.
a.
1.57 × 106
b.
2.77 × 10–3
c.
7.76 × 10–2
d.
1.17 × 10–3
39.
a.
4.34 × 105
b.
9.34 × 104
c.
9.916 × 101
d.
9.327 × 100
40.
a.
3.42 × 10–4
b.
1.034 × 104
7

Chapter 2: Measurements and Calculations
c.
1.7992 × 101
d.
3.37 × 105
41.
Since the only operations in the calculation are multiplication and division, the number of
significant figures is limited by the factor of 0.15 that has only two significant figures.
42.
170. mL;
18 mL limits the precision to the ones place, thus the answer is rounded to 170. mL
43.
three (based on 2.31 having 3 significant figures)
44.
three; (b), (c), and (d); (a) contains two significant figures
45.
two decimal places (based on 2.11 being known only to the second decimal place)
46.
none (10,434 is only known to the nearest whole number)
47.
a.
52.36 (the answer can only be given to the second decimal place because 0.81 is only
known to the second decimal place)
b.
10.90 (the answer can only be given to the second decimal place because 2.21 is only
known to the second decimal place)
c.
5.25 (the answer can only be given to the second decimal place because 4.14 is only
known to the second decimal place)
d.
6.5 (the answer can only be given to two significant figures because 3.1 is only known to
two significant figures.
48.
a.
2.3 (the answer can only be given to two significant figures because 3.1 is only known to
two significant figures)
b.
9.1 × 102: (the answer can only be given to the first decimal place because 4.1 is only
given to the first decimal place; both numbers have the same power of ten)
c.
1.323 × 103: (the numbers must be first expressed as the same power of ten;
1.091 × 103 + 0.221 × 103 + 0.0114 × 103 = 1.323 × 103)
d.
6.63 × 10–13 (the answer can only be given to three significant figures because 4.22 × 106
is only given to three significant figures)
49.
a.
two (based on 1.1 having only two significant figures)
b.
two (based on 0.22 having only 2 significant figures)
c.
two (based on 0.00033 having only two significant figures)
d.
three (assuming sum in numerator is considered to second decimal place)
8

Chapter 2: Measurements and Calculations
50.
a.
one (the factor of 2 has only one significant figure)
b.
four (the sum within the parentheses will contain four significant figures)
c.
two (based on the factor 4.7 10–6 only having two significant figures)
d.
three (based on the factor 63.9 having only three significant figures)
51.
a.
two (the factor of 2.1 has only two significant figures)
b.
two (the factor of 0.98 has only two significant figures)
c.
four (the factor of 3.014 has only four significant figures)
d.
three (the factor of 1.86 × 10–3 has only three significant figures)
52.
a.
(2.0944 + 0.0003233 + 12.22)/7.001 = (14.31)/7.001 = 2.045
b.
(1.42 102 + 1.021 103)/(3.1 10–1) =
(142 + 1021)/(3.1 10–1) = (1163)/(3.1 10–1) = 3752 = 3.8 103
c.
(9.762 10–3)/(1.43 102 + 4.51 101) =
(9.762 10–3)/(143 + 45.1) = (9.762 10–3)/(188.1) = 5.19 10–5
d.
(6.1982 10–4)2 = (6.1982 10–4)(6.1982 10–4) = 3.8418 10–7
53.
conversion factor
54.
an infinite number (a definition)
55.
1 mi
1760 yd
and
1760 yd
1 mi
56.
57.
58.
59.
a.
12.5 in
2.54 cm
1 in
= 31.8 cm
b.
12.5 cm
1 in
2.54 cm
= 4.92 in
c.
2513 ft
1 mi
5280 ft
= 0.4759 mi
9

Chapter 2: Measurements and Calculations
d.
4.53 ft
1 yd
1 m
3 ft
1.0936 yd
= 1.38 m
e.
6.52 min
60 sec
1 min
= 391 sec
f.
52.3 cm
1 m
100 cm
= 0.523 m
g.
4.21 m
1.0936 yd
1 m
= 4.60 yd
h.
8.02 oz
1 lb
16 oz
= 0.501 lb
60.
a.
2.23 m
= 2.44 yd
b.
46.2 yd
= 42.2 m
c.
292 cm
= 115 in
d.
881.2 in
= 2238 cm
e.
1043 km
= 648.1 mi
f.
445.5 mi
= 716.9 km
g.
36.2 m
= 0.0362 km
h.
0.501 km
= 5.01 104 cm
61.
a.
1.75 mi
1.6093 km
1 mi
= 2.82 km
b.
2.63 gal
4 qt
1 gal
= 10.5 qt
c.
4.675 cal
4.184 J
1 cal
= 19.56 J
d.
756.2 mm Hg
1 atm
760 mm Hg
= 0.9950 atm
10

Chapter 2: Measurements and Calculations
e.
36.3 amu
27
1.66056 10 kg
1 amu
= 6.03 × 10–26 kg
f.
46.2 in
2.54 cm
1 in
= 117 cm
g.
2.75 qt
32 fl oz
1 qt
= 88.0 fl oz
h.
3.51 yd
1 m
1.0936 yd
= 3.21 m
62.
a.
254.3 g ×
= 0.2543 kg
b.
2.75 kg ×
= 2750 g
c.
2.75 kg ×
= 6.06 lb
d.
2.75 kg ×
×
= 97.0 oz
e.
534.1 g ×
×
= 1.177 lb
f.
1.75 lb ×
×
= 794 g
g.
8.7 oz ×
453.59 g
16 oz
= 250 g
h.
45.9 g ×
= 1.62 oz
63.
1.89 × 1025 C atoms ×
23
12.01 g
6.02 10 C atoms
= 377 g
64.
2558 mi ×
1.6093 km
1 mi
= 4117 km
65.
To decide which train is faster, both speeds must be expressed in the same unit of distance (either
miles or kilometers).
225 km
1 mi
1 hr
1.6093 km
= 140. mi/hr
So the Boston-New York trains will be faster.
11

Chapter 2: Measurements and Calculations
66.
1 10–10 m
100 cm
1 m
= 1 10–8 cm
1 10–8 cm
1 in
2.54 cm
= 4 10–9 in.
1 10–8 cm
9
1 m
10 nm
100 cm
1 m
= 0.1 nm
67.
Celsius
68.
freezing
69.
212ºF; 100ºC
70.
373
71.
100
72.
Fahrenheit (F)
73.
K
C
C
K
= + 273
273
T
T
T
T
a.
44.2°C + 273 = 317.2 K (317 K)
b.
891 K – 273 = 618ºC
c.
–20°C + 273 = 253 K
d.
273.1 K – 273 = 0.1ºC (0°C)
74.
C
F
= ( 32)/1.80
T
T
K
C
C
K
= + 273
273
T
T
T
T
a.
b.
c.
d.
75.
C
F
= ( 32)/1.80
T
T
a.
(45 – 32)/1.80 = 13/1.80 = 7.2ºC
b.
(115 – 32)/1.80 = 83/1.80 = 46ºC
c.
(–10 – 32)/1.80 = –42/1.80 = –23ºC
d.
Assuming 10,000ºF to be known to two significant figures: (10,000 – 32)/1.80 = 5500ºC
76.
F
C
1.80( ) 32
T
T
12

Chapter 2: Measurements and Calculations
a.
1.80(78.1) + 32 = 173ºF
b.
1.80(40.) + 32 = 104ºF
c.
1.80(–273) + 32 = –459ºF
d.
1.80(32) + 32 = 90.ºF
77.
a.
Gallium is in the liquid state over the temperature range of this thermometer.
b.
F
C
1.80( ) 32
T
T
TF = 1.80(50°C) + 32 = 122°F
TF = 1.80(500°C) + 32 = 932°F
78.
F
C
1.80( ) 32
T
T
C
F
= ( 32)/1.80
T
T
TK = TC + 273
a.
275 – 273 = 2ºC
b.
(82 – 32)/1.80 = 28ºC
c.
1.80(–21) + 32 = –5.8ºF (–6ºF)
d.
(–40 – 32)/1.80 = –40 ºC (Celsius and Fahrenheit temperatures are the same at –40).
79.
Density represents the mass per unit volume of a substance.
80.
g/cm3 (g/mL)
81.
lead
82.
100 in.3
83.
smaller; gases are mostly empty space, so there is less mass in a given volume than for solids and
liquids.
84.
Density is a characteristic property, which is always the same for a pure substance.
85.
Gold is the most dense; hydrogen is the least dense; 1 g of hydrogen would occupy the larger
volume.
86.
Silver is the most dense (10.5 g/cm3).
87.
density =
mass
volume
a.
d =
3
452.1 g
292 cm
= 1.55 g/cm3
b.
m = 0.14 lb = 63.5 g v = 125 mL = 125 cm3
d =
3
63.5 g
125 cm
= 0.51 g/cm3
c.
m = 1.01 kg = 1010 g
13

Chapter 2: Measurements and Calculations
d =
3
1010 g
1000 cm
= 1.01 g/cm3
d.
m = 225 mg = 0.225 g v = 2.51 mL = 2.51 cm3
d =
3
0.225 g
2.51 cm
= 0.0896 g/cm3
88.
density =
mass
volume
a.
m = 4.53 kg
1000 g
1 kg
= 4530 g
b.
v = 25.0 mL
= 25.0 cm3
c.
m = 1.00 lb
1000 g
1 kg
= 454 g
d.
m = 352 mg
= 0.352 g
89.
125 mL
3.12 g
1 mL
= 390. g
85.0 g ×
1 mL
3.12 g
= 27.2 mL
90.
4.50 L
= 4140 g
375 g
= 0.408 L
91.
d =
assuming 1000 mL is exact.
14

Chapter 2: Measurements and Calculations
92.
m = 3.5 lb
453.59 g
1 lb
= 1.59 103 g
v = 1.2 104 in.3
3
2.54 cm
1 in
= 1.97 105 cm3
d =
3
5
3
1.59 10 g
1.97 10 cm
= 8.1 10–3 g/cm3
The material will float.
93.
The volume of the iron can be calculated from its mass and density:
v = 52.4 g
3
1 cm
7.87 g
= 6.66 cm3 = 6.66 mL.
The liquid level in the graduated cylinder will rise by 6.66 mL when the piece of iron is added,
giving a final volume of (75.0 + 6.66) = 81.7 mL
94.
25.75 g
= 1.333 cm3 = 1.333 mL
13.3 mL + 1.333 mL = 14.6 mL
95.
a.
50.0 g
3
1 cm
2.16 g
= 23.1 cm3
b.
50.0 g
3
1 cm
13.6 g
= 3.68 cm3
c.
50.0 g
3
1 cm
0.880 g
= 56.8 cm3
d.
50.0 g
3
1 cm
10.5 g
= 4.76 cm3
96.
a.
50.0 cm3
3
19.32 g
1 cm
= 966 g
b.
50.0 cm3
3
7.87 g
1 cm
= 394 g
c.
50.0 cm3
3
11.34 g
1 cm
= 567 g
d.
50.0 cm3
3
2.70 g
1 cm
= 135 g
97.
a.
three
b.
three
15

Chapter 2: Measurements and Calculations
c.
three
98.
a.
3.011 1023 = 301,100,000,000,000,000,000,000
b.
5.091 109 = 5,091,000,000
c.
7.2 102 = 720
d.
1.234 105 = 123,400
e.
4.32002 10–4 = 0.000432002
f.
3.001 10–2 = 0.03001
g.
2.9901 10–7 = 0.00000029901
h.
4.2 10–1 = 0.42
99.
a.
4.25 102
b.
7.81 10–4
c.
2.68 104
d.
6.54 10–4
e.
7.26 101
100.
(e)
101.
a.
1.25 in.
1 ft
12 in
= 0.104 ft
1.25 in.
2.54 cm
1 in
= 3.18 cm
b.
2.12 qt
1 gal
4 qt
= 0.530 gal
2.12 qt
1 L
1.0567 qt
= 2.01 L
c.
2640 ft
1 mi
5280 ft
= 0.500 mi
2640 ft
1.6093 km
5280. ft
= 0.805 km
d.
1.254 kg
3
3
10 g
1 cm
1 kg
11.34 g
= 110.6 cm3
e.
250. mL 0.785 g/mL = 196 g
f.
3.5 in.3
3
2.54 cm
1 in
= 57 cm3 = 57 mL
57 cm3 13.6 g/cm3 = 7.8 102 g = 0.78 kg
16

Chapter 2: Measurements and Calculations
102.
a.
36.2 blim
1400 kryll
1 blim
= 5.07 104 kryll
b.
170 kryll
1 blim
1400 kryll
= 0.12 blim
c.
72.5 kryll2
2
1 blim
1400 kryll
= 3.70 10–5 blim2
103.
110 km
1 hr
100 km
= 1.1 hr
104.
105.
45 mi
1.6093 km
1 mi
= 72.4 km
38 mi
1.6093 km
1 mi
= 61.2 km
1 gal = 3.7854 L
highway: 72.4 km/3.7854 L = 19 km/L
city: 61.2 km/3.7854 L = 16 km/L
106.
107.
15.6 g
1 capsule
0.65 g
= 24 capsules
108.
°X = 1.26C + 14
109.
3
4
3
v
r
4
3 (3.1416)(0.5 cm)
3 = 0.52 cm3
d =
3
2.0 g
0.52 cm
= 3.8 g/cm3 (the ball will sink)
110.
d =
36.8 g
10.5 L
= 3.50 g/L (3.50 10–3 g/cm3)
111.
a.
25.0 g
3
1 cm
0.000084 g
= 2.98 105 cm3
b.
25.0 g
3
1 cm
13.6 g
= 1.84 cm3
17

Chapter 2: Measurements and Calculations
c.
25.0 g
3
1 cm
11.34 g
= 2.20 cm3
d.
25.0 g
3
1 cm
1.00 g
= 25.0 cm3
112.
For ethanol, 100. mL
0.785 g
1 mL
= 78.5 g
For benzene, 1000 mL
0.880 g
1 mL
= 880. g
total mass, 78.5 + 880. = 959 g
113.
three
114.
a.
negative
b.
negative
c.
positive
d.
zero
e.
negative
115.
a.
positive
b.
negative
c.
negative
d.
zero
116.
a.
2; positive
b.
11; negative
c.
3; positive
d.
5; negative
e.
5; positive
f.
0; zero
g.
1; negative
h.
7; negative
117.
a.
4; positive
b.
6; negative
c.
0; zero
d.
5; positive
e.
2; negative
18

Chapter 2: Measurements and Calculations
118.
a.
1; positive
b.
3; negative
c.
0; zero
d.
3; positive
e.
9; negative
119.
a.
The decimal point must be moved two places to the left, so the exponent is positive 2;
529 = 5.29 102.
b.
The decimal point must be moved eight places to the left, so the exponent is positive 8;
240,000,000 = 2.4 108.
c.
The decimal point must be moved 17 places to the left, so the exponent is positive 17;
301,000,000,000,000,000 = 3.01 1017.
d.
The decimal point must be moved four places to the left, so the exponent is positive 4;
78,444 = 7.8444 104.
e.
The decimal point must be moved four places to the right, so the exponent is negative 4;
0.0003442 = 3.442 10–4.
f.
The decimal point must be moved 10 places to the right, so the exponent is negative 10;
0.000000000902 = 9.02 10–10.
g.
The decimal point must be moved two places to the right, so the exponent is negative 2;
0.043 = 4.3 10–2.
h.
The decimal point must be moved two places to the right, so the exponent is negative 2;
0.0821 = 8.21 10–2.
120.
a.
The decimal point must be moved five places to the left; 2.98 10–5 = 0.0000298.
b.
The decimal point must be moved nine places to the right; 4.358 109 = 4,358,000,000.
c.
The decimal point must be moved six places to the left; 1.9928 10–6 = 0.0000019928.
d.
The decimal point must be moved 23 places to the right; 6.02 1023 =
602,000,000,000,000,000,000,000.
e.
The decimal point must be moved one place to the left; 1.01 10–1 = 0.101.
f.
The decimal point must be moved three places to the left; 7.87 10–3 = 0.00787.
g.
The decimal point must be moved seven places to the right; 9.87 107 = 98,700,000.
h.
The decimal point must be moved two places to the right; 3.7899 102 = 378.99.
i.
The decimal point must be moved one place to the left; 1.093 10–1 = 0.1093.
j.
The decimal point must be moved zero places; 2.9004 100 = 2.9004.
k.
The decimal point must be moved four places to the left; 3.9 10–4 = 0.00039.
l.
The decimal point must be moved eight places to the left; 1.904 10–8 = 0.00000001904.
121.
To say that scientific notation is in standard form means that you have a number between 1 and
10, followed by an exponential term. The numbers given in this problem are not between 1 and
10 as written.
19
Chapter 2: Measurements and Calculations
a.
102.3 10–5 = (1.023 102) 10–5 = 1.023 10–3
b.
32.03 10–3 = (3.203 101) 10–3 = 3.203 10–2
c.
59933 102 = (5.9933 104) 102 = 5.9933 106
d.
599.33 104 = (5.9933 102) 104 = 5.9933 106
e.
5993.3 103 = (5.9933 103) 103 = 5.9933 106
f.
2054 10–1 = (2.054 103) 10–1 = 2.054 102
g.
32,000,000 10–6 = (3.2 107) 10–6 = 3.2 101
h.
59.933 105 = (5.9933 101) 105 = 5.9933 106
122.
a.
1/102 = 1 10–2
b.
1/10–2 = 1 102
c.
55/103 =
1
3
5.5 10
1 10
= 5.5 10–2
d.
(3.1 106)/10–3 =
6
3
3.1 10
1 10
= 3.1 109
e.
(106)1/2 = 1 103
f.
(106)(104)/(102) =
6
4
2
(1 10 )(1 10 )
(1 10 )
= 1 108
g.
1/0.0034 =
-3
1
3.4 10
= 2.9 102
h.
3.453/10–4 =
-4
3.453
1 10
= 3.453 104
123.
meter
124.
125.
100 km (See inside cover of textbook.)
126.
1 L = 1 dm3 = 1000 cm3 = 1000 mL
127.
250. mL
128.
0.105 m
20

Chapter 2: Measurements and Calculations
129.
100 km/hr = 62.1 mi/hr; you would not violate the speed limit.
130.
They weigh the same.
131.
4.25 g (425 mg = 0.425 g)
132.
51011 nm
133.
volume
134.
v = l h w
0.310 m3 = (0.7120 m)(0.52458 m) w
w = 0.830 m (The answer is to three significant figures because the final volume of the box is
reported to three significant figures. The other two measurements contain more significant figures
and do not limit the precision of the volume.)
135.
a.
one
b.
one
c.
four
d.
two
e.
infinite (definition)
f.
one
136.
a.
0.000426
b.
4.02 10–5
c.
5.99 106
d.
400.
e.
0.00600
137.
a.
0.7556
b.
293
c.
17.01
d.
432.97
138.
a.
2149.6 (the answer can only be given to the first decimal place, because 149.2 is only
known to the first decimal place)
21

Chapter 2: Measurements and Calculations
b.
5.37 103 (the answer can only be given to two decimal places because 4.34 is only
known to two decimal places; moreover, since the power of ten is the same for each
number, the calculation can be performed directly)
c.
Before performing the calculation, the numbers have to be converted so that they contain
the same power of ten.
4.03 10–2 – 2.044 10–3 = 4.03 10–2 – 0.2044 10–2 = 3.83 10–2 (the answer can
only be given the second decimal place because 4.03 10–2 is only known to the second
decimal place)
d.
Before performing the calculation, the numbers have to be converted so that they contain
the same power of ten.
2.094 105 – 1.073 106 = 2.094 105 – 10.73 105 = –8.64 105
139.
a.
5.57 107 (the answer can only be given to three significant figures because 0.0432 and
4.43 108 are only known to three significant figures)
b.
2.38 10–1 (the answer can only be given to three significant figures because 0.00932
and 4.03 102 are only known to three significant figures)
c.
4.72 (the answer can only be given to three significant figures because 2.94 is only
known to three significant figures)
d.
8.08 108 (the answer can only be given to three significant figures because 0.000934 is
only known to three significant figures)
140.
a.
(2.9932 104)(2.4443 102 + 1.0032 101) =
(2.9932 104)(24.443 101 + 1.0032 101) =
(2.9932 104)(25.446 101) = 7.6166 106
b.
(2.34 102 + 2.443 10–1)/(0.0323) =
(2.34 102 + 0.002443 102)/(0.0323) =
(2.34 102)/(0.0323) = 7.24 103
c.
(4.38 10–3)2 = 1.92 10–5
d.
(5.9938 10–6)1/2 = 2.4482 10–3
141.
3
3
1 L
1000 cm
;
1000 cm
1 L
142.
1 year
12 months
;
12 months
1 year
143.
a.
8.43 cm
10 mm
1 cm
= 84.3 mm
b.
2.41 102 cm
1 m
100 cm
= 2.41 m
c.
294.5 nm
9
1 m
100 cm
10 nm
1 m
= 2.945 10–5 cm
22

Chapter 2: Measurements and Calculations
d.
404.5 m
1 km
1000 m
= 0.4045 km
e.
1.445 104 m
1 km
1000 m
= 14.45 km
f.
42.2 mm
1 cm
10 mm
= 4.22 cm
g.
235.3 m
1000 mm
1 m
= 2.353 105 mm
h.
903.3 nm
6
9
1 m
10 μm
10 nm
1m
= 0.9033 m
144.
a.
908 oz
1 lb
1 kg
16 oz 2.2046 lb
= 25.7 kg
b.
12.8 L
1 qt
1 gal
0.94633 L
4 qt
= 3.38 gal
c.
125 mL
1 L
1 qt
1000 mL 0.94633 L
= 0.132 qt
d.
2.89 gal
4 qt
1 L
1000 mL
1 gal 1.0567 qt
1 L
= 1.09 104 mL
e.
4.48 lb
453.59 g
1 lb
= 2.03 103 g
f.
550 mL
1 L
1.0567 qt
1000 mL
1 L
= 0.58 qt
145.
9.3 107 mi
1 km
0.62137 mi
= 1.5 108 km
1.5 108 km
1000 m 100 cm
1 km
1 m
= 1.5 1013 cm
146.
5.3103 lbs
1 kg
2.2046 lbs
1 metric ton
1000 kg
= 2.4 metric tons
23

Chapter 2: Measurements and Calculations
147.
K
C
273
T
T
a.
0 + 273 = 273 K
b.
25 + 273 = 298 K
c.
37 + 273 = 310. K
d.
100 + 273 = 373 K
e.
–175 + 273 = 98 K
f.
212 + 273 = 485 K
148.
a.
Celsius temperature = (175 – 32)/1.80 = 79.4C
Kelvin temperature = 79.4 + 273 = 352 K
b.
255 – 273 = –18 C
c.
(–45 – 32)/1.80 = –43C
d.
1.80(125) + 32 = 257F
149.
density =
mass
volume
a.
d =
3
234 g
2.2 cm
= 110 g/cm3
b.
m = 2.34 kg
1000 g
1 kg
= 2340 g
v = 2.2 m3
3
100 cm
1 m
= 2.2 106 cm3
d =
6
3
2340 g
2.2 10 cm
= 1.1 10–3 g/cm3
c.
m = 1.2 lb
453.59 g
1 lb
= 544 g
v = 2.1 ft3
3
12 in
1 ft
3
2.54 cm
1 in
= 5.95 104 cm3
d =
4
3
544 g
5.95 10 cm
= 9.1 10–3 g/cm3
24

Chapter 2: Measurements and Calculations
d.
m = 4.3 ton
2000lb 453.59 g
1 ton
1 lb
= 3.90 106 g
v = 54.2 yd3
3
1 m
1.0936 yd
3
100 cm
1 m
= 4.14 107 cm3
d =
6
7
3
3.90 10 g
4.14 10 cm
= 9.4 10–2 g/cm3
150.
85.5 mL
0.915 g
1 mL
= 78.2 g
151.
50.0 g
1 mL
1.31 g
= 38.2 g
152.
m = 155 lb
453.59 g
1 lb
= 7.031 104 g
v = 4.2 ft3
3
12 in
1 ft
3
2.54 cm
1 in
= 1.189 105 cm3
d =
4
5
3
7.031 10 g
1.189 10 cm
= 0.59 g/cm3
153.
Volume = 21.6 mL – 12.7 mL = 8.9 mL
d =
33.42 g
8.9 mL
= 3.8 g/mL
154.
F
C
1.80( ) 32
T
T
a.
23 F
b.
32 F
c.
–321 F
d.
–459 F
e.
187 F
f.
–459 F
155.
a.
103
b.
109
c.
10–2
d.
10–3
156.
a.
The Mars Climate Orbiter dipped 100 km lower in the Mars atmosphere than was
planned. Using the conversion factor between miles and kilometers found inside the
cover of this text
25

Chapter 2: Measurements and Calculations
1 mi
100 km
= 62 mi
1.6093 km
b.
The aircraft required 22,300 kg of fuel, but only 22,300 lb of fuel was loaded. Using the
conversion factor between pounds and kilograms found inside the cover of this text, the
amount of fuel required in pounds was
2.2046 lb
22,300 kg
= 49, 163 lb
1 kg
Therefore, (49,163 – 22,300) = 26,863 = 2.69 × 104 lb additional fuel was needed.
157.
a.
The text mentions oxygen sensors in automobile exhaust systems; detection of nitrogen-
containing compounds in airline baggage; use of sensory hair from crabs to detect low
levels of hormones; use of pineapple extracts to detect hydrogen peroxide
b.
We can now detect the presence of impurities or contaminants to much lower levels than
was possible in the past. Although that may seem helpful, we now have to determine
whether these contaminants were always present and are not harmful or if they are
something new that we should be concerned about.
158.
8
11
10 g
1 lb
1 L
4 qt
= 8 10 lb/gal
L
453.59 g
1.0567 qt
1 gal
159.
Scientific Notation
Number of Significant Figures
9.000102
4
3.007103
4
2.345104
4
2.700102
4
4.37105
3
160.
Number of Significant Figures
Result
2
0.51
3
29.1
3
8.61
3
1.89
4
134.6
3
14.4
161.
26

Chapter 2: Measurements and Calculations
162.
60 sec + 59.2 sec = 119.2 sec
163.
C
F
= ( 32)/1.80
T
T
TC = (69.1 – 32)/1.80 = 20.6ºC
164.
C
F
= ( 32)/1.80
T
T
TC = (134 – 32)/1.80 = 56.7ºC
Since the temperature is higher than the melting point (44ºC), phosphorus would be a liquid.
165.
1.84 cm 3.61 cm 2.10 cm = 13.9 cm3
166.
27