
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Computer Graphics and Programming
Quaternion
Jeong-Yean Yang
2020/10/22
1
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
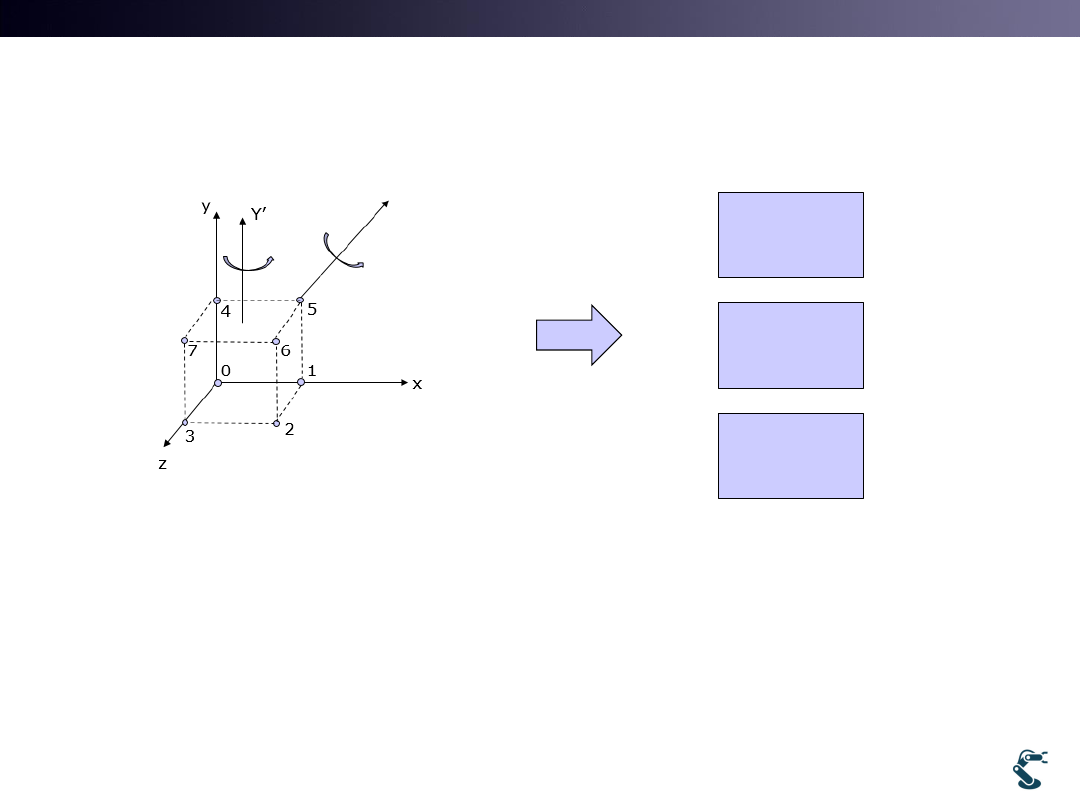
Problem of Rotation along an Arbitrary Axis
• Homogeneous Transform needs
– We find proper Rotation and Rotation for an Arbitrary Axis
It is NOT Easy
– Reminds HW 10
• How we do it Easily Quaternion by Hamilton
2
Rotation
Along 3-5
Y’=RotX(Y)
RotZ(Y’)
Complex
Angle
Calculation

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
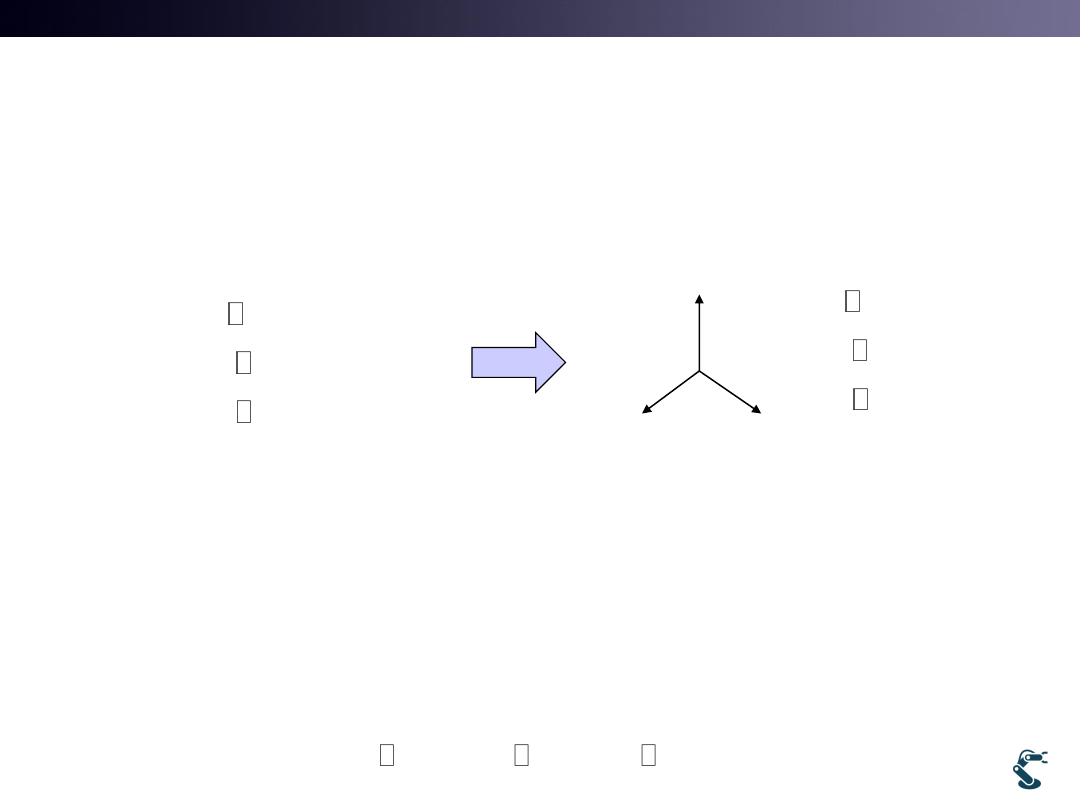
Quaternion
• Quaternion is a Four Dimensional Complex Number
– Remind we learn 2 Dim Complex number
• Quaternion has
– 1 scalar value(Real Part)
– 3 dimensional Imaginary Part
– Imaginary pat is a 3 Dim. vector
3
q
s
xi
yj
zk
q
Z
real
imaginary
z
Z
z
x
yi
Re( )
q
s
Im( )
( , , )
q
x y z
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Quaternion has three imaginary part, i, j, k
• Main idea is that i, j, and k are Orthogonal as in XYZ
3D space
• Similar to Cross Product.
4
1
1
1
i i
j j
k k
Same as in Complex number
q
s
xi
yj
zk
3D Axis
i
j
k
i j
k
j k
i
k i
j
Defining i*j = k
that i, j, and k
are orthogonal
,
,
i
j
j
k
k
i
,
,
j i
k
k j
i
i k
j
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Quaternion Basic Form
• Quaternion has one scalar(Angle) and one Vector(axis)
• Quaternion Addition
5
(
)
ˆ
( , )
q
s
xi
yj
zk
s
xi
yj
zk
s u
ˆu
s
1
1
1
1
1
2
2
2
2
2
1
2
1
2
1
2
1
2
1
2
,
(
) (
)
(
)
(
)
q
s
x i
y j
z k
q
s
x i
y j
z k
q
q
s
s
x
x i
y
y
j
z
z k
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Quaternion Multiplication (1)
6
1
2
1
1
1
1
2
2
2
2
1 2
1 2
1
2
1 2
2
1 2
1 2
1
2
1 2
2
1 2
1 2
1
2
1 2
2
1 2
1 2
1
2
1 2
q q
s
x i
y j
z k
s
x i
y j
z k
s s
s x i
s y j
s z k
x s i
x x i
x y ij
x z ik
y s j
y x ji
y y j
y z jk
z s k
z x ki
z y kj
z z k
1 2
1 2
1
2
1 2
1 2
1 2
1
2
1 2
1 2
1 2
1
2
1 2
1 2
1 2
1
2
1 2
s s
s x i
s y j
s z k
x s i
x x
x y k
x z j
y s j
y x k
y y
y z i
z s k
z x j
z y i
z z
1
1
1
1
1
2
2
2
2
2
,
q
s
x i
y j
z k
q
s
x i
y j
z k
i j
k
j k
i
k i
j
j i
k
k j
i
i k
j

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Quaternion Multiplication (2)
• Magnitude of Quaternion
– Remind |Z|
7
1
2
1 2
1 2
1
2
1 2
1 2
1
2
1 2
2 1
2
1
2 1
1 2
1
2
1 2
1 2
1
2
1 2
q q
s s
x x
y y
z z
s x i
s y j
s z k
s x i
s y j
s z k
y z
z y i
z x
x z
j
x y
y x
k
2
ˆ
( ,
)
ˆ
ˆ
ˆ
ˆ ˆ
ˆ
(
)
ˆ ˆ
q
s
u
q q
ss u
u
su
su
u
u
s
u u
1
2
1 2
1
2
1 2
2 1
1
2
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
'
'
Q
q q
s s
u
u
s u
s u
u
u
s
u
2
| |
|
|
z
zz

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Unit Quaternion
• Magnitude of Complex Variable Quaternion |q|
– Remind |z|
– Magnitude of Quaternion
• Definition of Pure Quaternion: s=0
• Definition of Unit Quaternion(Versor) :
8
2
| |
|
|
z
zz
1
2
1 2
1
2
1 2
2 1
1
2
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
'
'
Q
q q
s s
u
u
s u
s u
u
u
s
u
2
ˆ
ˆ
ˆ
ˆ ˆ
ˆ
(
)
ˆ ˆ
q q
ss u
u
su
su
u
u
s
u u
ˆ
(0, )
p
q
u
ˆ
( ,
)
q
s
u
ˆ ˆ
|
| |
|
q q
u u
|
| 1
u
q
2
ˆ ˆ
|
| |
| 1
q q
s
u u
ˆ
( , )
q
s u

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Inverse Quaternion
• Inverse Quaternion is derived from Magnitude Equation
• If q is an unit quaternion,
9
2
1
2
|| ||
|| ||
q
q q
q
q
q
2
1
2
|| ||
|| ||
q
q q
q
q
q
q
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
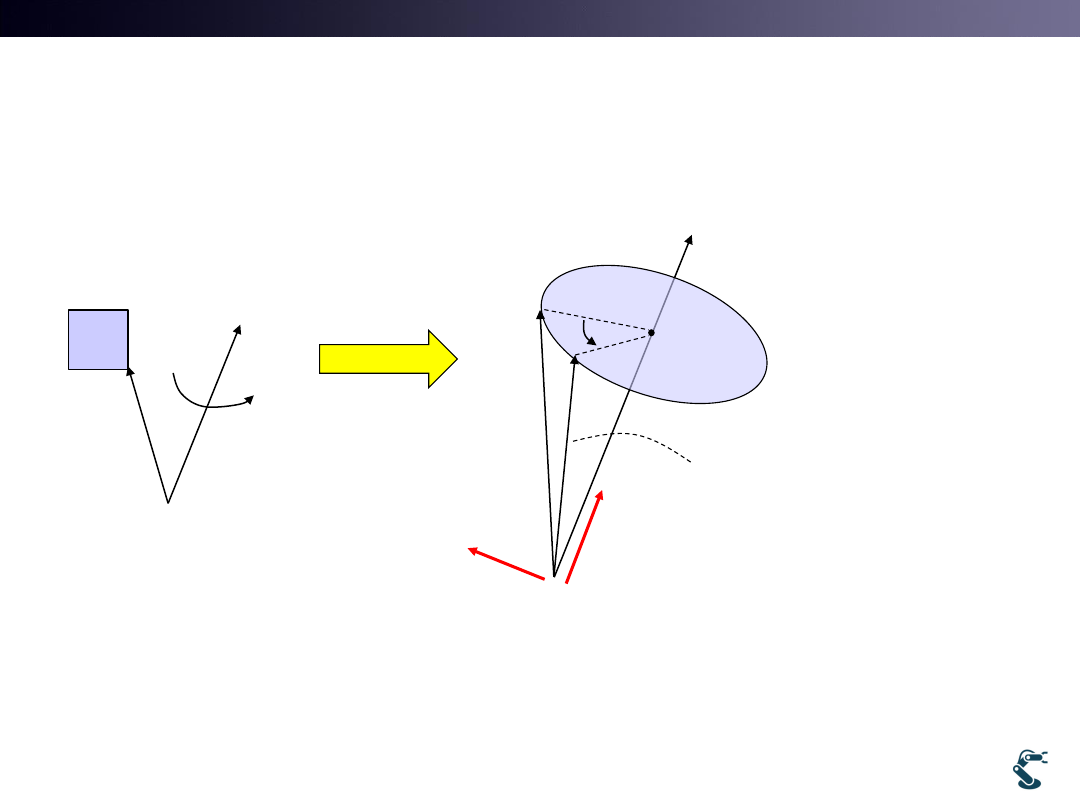
Let’s go Back to Arbitrary Rotation
by Vector Calculus (NOT Quaternion)
10
ˆu
s
ˆu
ˆv
vertex
ˆv
ˆ
t
v
ˆ
s
v
ˆ
ˆ
:
ˆ
ˆ
:
t
s
v Parallel to u
v
Perpendicular to u
ˆ
ˆ
'
( )
v
R v
ˆ
ˆ
ˆ
ˆ
'
( )
( )
( )
s
t
v
R v
R v
R v
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
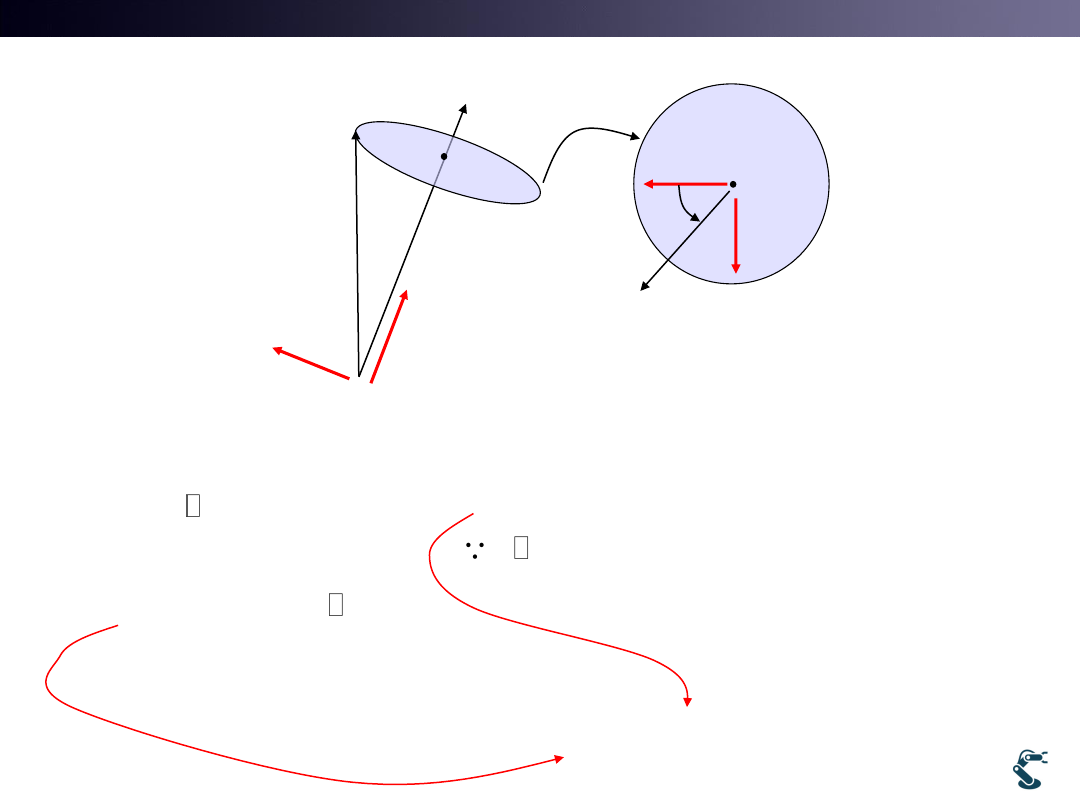
11
ˆu
ˆv
ˆ
t
v
ˆ
s
v
ˆu
ˆ
s
v
ˆw
rotation
ˆ
ˆ ˆ ˆ
(
)
ˆ
ˆ
ˆ
ˆ
ˆ ˆ
ˆ
ˆ ˆ ˆ
(
)
t
t
s
s
t
v
v u u
v
v
v
v
v v
v
v u u
Derive Vs
Derive w
ˆ
ˆ ˆ
ˆ
ˆ ˆ
ˆ ˆ ˆ ˆ
ˆ ˆ
ˆ ˆ
ˆ ˆ
0,
s
t
t
t
t
w
u v
u
v v
u v u v
u v
u v
u v
ˆ
( )
s
R v
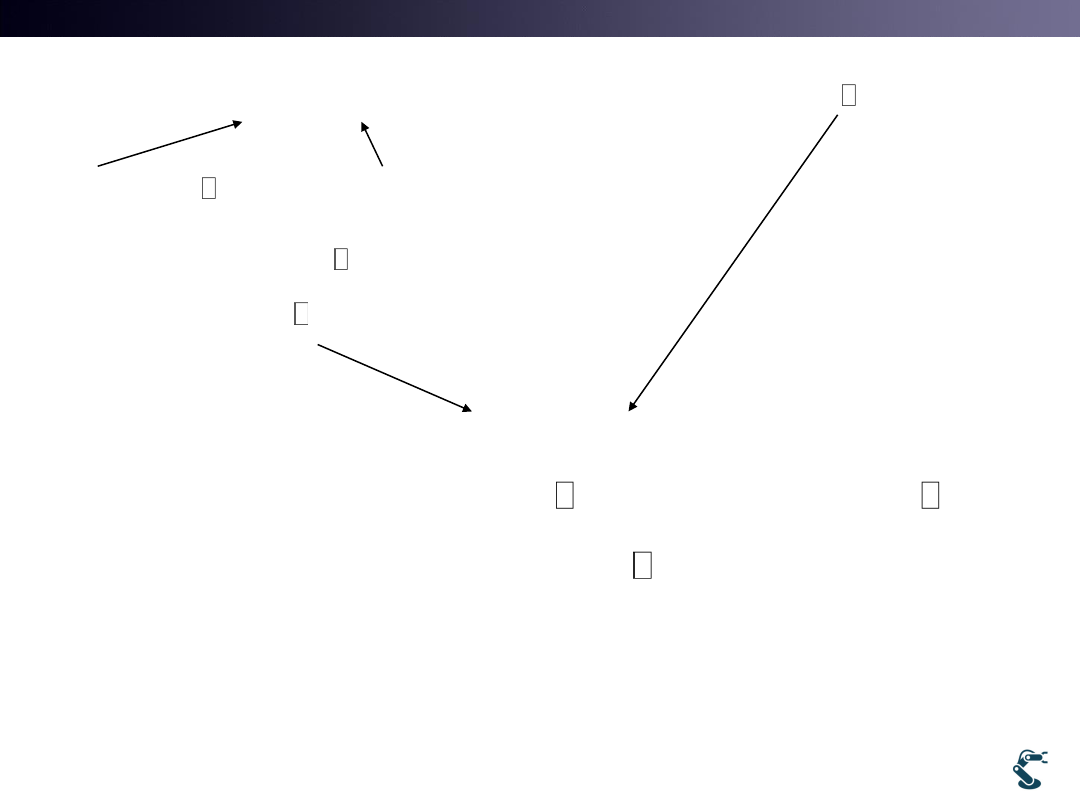
Derive Rotation, in plane
ˆ
( )
s
R v
ˆ ˆ
,
s
v w
ˆ
ˆ
ˆ
( )
cos
sin
s
s
R v
v
w
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
12
ˆ
ˆ
ˆ
( )
cos
sin
s
s
R v
v
w
ˆ
ˆ
ˆ ˆ ˆ
(
)
s
v
v
v u u
ˆ
ˆ ˆ
w
u v
ˆ
ˆ
ˆ ˆ ˆ
ˆ ˆ
( )
cos
(
)
sin
ˆ
ˆ ˆ ˆ
ˆ ˆ
cos
cos (
)
sin
s
R v
v
v u u
u v
v
v u u
u v
ˆ
ˆ
ˆ
ˆ
'
( )
( )
( )
s
t
v
R v
R v
R v
ˆ
ˆ
ˆ ˆ ˆ
( )
(
)
t
t
R v
v
v u u
ˆ
ˆ ˆ ˆ
ˆ ˆ
ˆ ˆ ˆ
cos
cos (
)
sin
(
)
ˆ
ˆ ˆ ˆ
ˆ ˆ
cos
(1 cos )(
)
sin
v
v u u
u v
v u u
v
v u u
u v
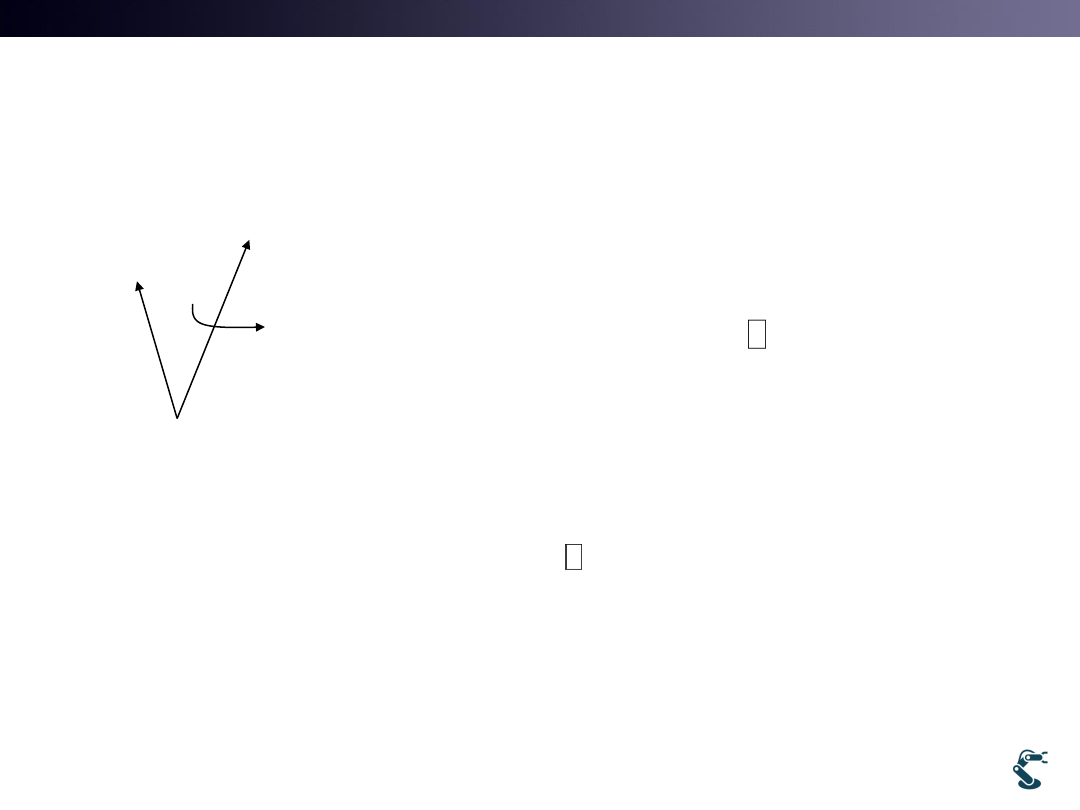
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Example of Rotation along an Arbitrary Axis
by Vector Calculus
• Think that x axis rotates along z axis with 90 degree.
13
ˆu
ˆv
vertex
ˆ
ˆ
ˆ ˆ ˆ
ˆ ˆ
'
cos
(1 cos )(
)
sin
Arbitrary Rotation
v
v
v u u
u v
ˆ
ˆ
ˆ
ˆ
ˆ ˆ
ˆ
'
0
(1 0)(
)
1
ˆ
ˆ
ˆ
0 0
x
x
x z z
z x
z
y
y

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
From Vector Calculus to Quaternion
14
ˆ
ˆ
ˆ
( , )
cos
sin
, | | 1
2
2
if q
s u
u
u
1
ˆ
ˆ
ˆ
: '
( )
Lemma v
R v
qvq
1
2
2
ˆ
ˆ
ˆ
ˆ ˆ
ˆ
'
cos
sin
cos
sin
2
2
2
2
ˆ
ˆ ˆ
ˆ
cos
sin
cos
, sin
2
2
2
2
ˆ
ˆ ˆ ˆ ˆ
ˆ ˆ ˆ
cos
(
) cos
sin
sin
2
2
2
2
v
qvq
qvq
u v
u
v
uv
u
v
uv vu
uvu
1
2
|| ||
q
q
q
q
2
2
2
ˆ ˆ
ˆ ˆ
|
| |
|
|
| cos
sin
1
2
2
q q
s
u u
q q
u u
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
15
1
2
2
ˆ
ˆ
'
ˆ
ˆ ˆ ˆ ˆ
ˆ ˆ ˆ
cos
(
) cos
sin
sin
2
2
2
2
v
qvq
v
uv vu
uvu
ˆ ˆ (
)(
)
ˆ ˆ (
)(
)
ˆ ˆ ˆ ˆ
x
y
z
x
y
z
x x
x
y
x z
y x
y
y
y z
z x
z
y
z z
x
y
z
x
y
z
x
x
x
y
x
z
y
x
y
y
y
z
z
x
z
y
z
z
x
y
x z
y x
y z
uv
u i u j
u k v i
v j
v k
u v
u v k
u v j u v k
u v
u v i u v j u v i u v
vu
v i
v j
v k u i u j
u k
v u
v u k
v u j
v u k
v u
v u i
v u j
v u i v u
uv vu
u v k
u v j u v k
u v i
(
)
(
)
(
)
ˆ ˆ
2(
)
z x
z
y
x
y
x
z
y
x
y
z
z
x
z
y
y z
z
y
y
z
z
y
x z
z x
x
z
z
x
x
y
y x
x
y
y
x
u v j u v i v u k
v u j
v u k
v u i v u j
v u i
u v
u v
v u
v u i
u v
u v
v u
v u
j
u v
u v
v u
v u k
u v
ˆ ˆ ˆ ˆ
ˆ ˆ
2(
)
ˆ ˆ ˆ
ˆ ˆ ˆ
ˆ ˆ ˆ
(
) 2 (
)
uv vu
u v
uvu
v u u
u u v
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
16
1
2
2
2
2
2
2
2
ˆ
ˆ
'
ˆ
ˆ ˆ
ˆ ˆ ˆ
ˆ ˆ ˆ
cos
2 cos
sin
(
) sin
(
) 2 (
)
2
2
2
2
ˆ
ˆ ˆ
ˆ
ˆ ˆ ˆ
cos
sin (
) sin
2 sin
(
)
2
2
2
ˆ
ˆ ˆ
ˆ ˆ ˆ
cos
sin
sin (
)
1 cos
(
)
2
2
ˆ
ˆ ˆ
ˆ ˆ ˆ
cos
sin (
)
1 cos
(
)
co
v
qvq
v
u v
v u u
u u v
v
u v
v
u u v
v
u v
u u v
v
u v
u u v
ˆ
ˆ ˆ ˆ
ˆ ˆ
s
1 cos
(
) sin (
)
v
u u v
u v
.13, Vector Calculus
ˆ
ˆ
ˆ
ˆ
'
( )
( )
( )
s
t
pp
v
R v
R v
R v
ˆ
ˆ ˆ ˆ
ˆ ˆ
ˆ ˆ ˆ
cos
cos (
)
sin
(
)
ˆ
ˆ ˆ ˆ
ˆ ˆ
cos
(1 cos )(
)
sin
v
v u u
u v
v u u
v
v u u
u v
1
ˆ
ˆ
ˆ
: '
( )
Lemma v
R v
qvq
ˆ
ˆ
cos
sin
, | | 1
2
2
if q
u
u

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Quaternion is Too Complex??
Yes, It is.
• Let’s move to Transform matrix from Quaternion
17
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Quaternion To Homogeneous Transform
18
ˆ
ˆ
cos
sin
, | | 1
(
2
2
ˆ
ˆ
'
)
q
u
v
R v
u
0
1
2
3
2
2
2
2
0
1
2
3
1 2
0
3
1 3
0
2
2
2
2
2
1 2
0
3
0
1
2
3
2
3
0 1
2
2
2
2
1 3
0
2
2
3
0 1
0
1
2
3
cos
sin
sin
sin
2
2
2
2
2(
)
2(
)
0
2(
)
2(
)
0
2(
)
2(
)
0
0
0
0
1
ˆ
ˆ
ˆ
'
(
x
y
z
q
u i
u j
u k
q
q i
q j
q k
q
q
q
q
q q
q q
q q
q q
q q
q q
q
q
q
q
q q
q q
H
q q
q q
q q
q q
q
q
q
q
v
Hv
R
)
v

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Three Results of Arbitrary Rotation
• Vector Calculus
• Quaternion Rotation
• Homogenous Transform
19
ˆu
ˆv
vertex
ˆ
ˆ
ˆ ˆ ˆ
ˆ ˆ
'
cos
(1 cos )(
)
sin
v
v
v u u
u v
1
ˆ
ˆ
'
ˆ
ˆ ˆ ˆ
ˆ ˆ
cos
1 cos
(
) sin (
)
v
qvq
v
u u v
u v
2
2
2
2
0
1
2
3
1 2
0
3
1 3
0
2
2
2
2
2
1 2
0
3
0
1
2
3
2
3
0 1
2
2
2
2
1 3
0
2
2
3
0 1
0
1
2
3
2(
)
2(
)
0
2(
)
2(
)
0
2(
)
2(
)
0
0
0
0
1
ˆ
ˆ
'
q
q
q
q
q q
q q
q q
q q
q q
q q
q
q
q
q
q q
q q
H
q q
q q
q q
q q
q
q
q
q
v
Hv

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Quaternion Homogeneous Transform
20