
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Robot Learning
3. Numerical Method-Regression
Jeong-Yean Yang
2020/10/22
1
T&C LAB-AI
Regression( or Fitting Problem)
Linear Problem
4
2
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
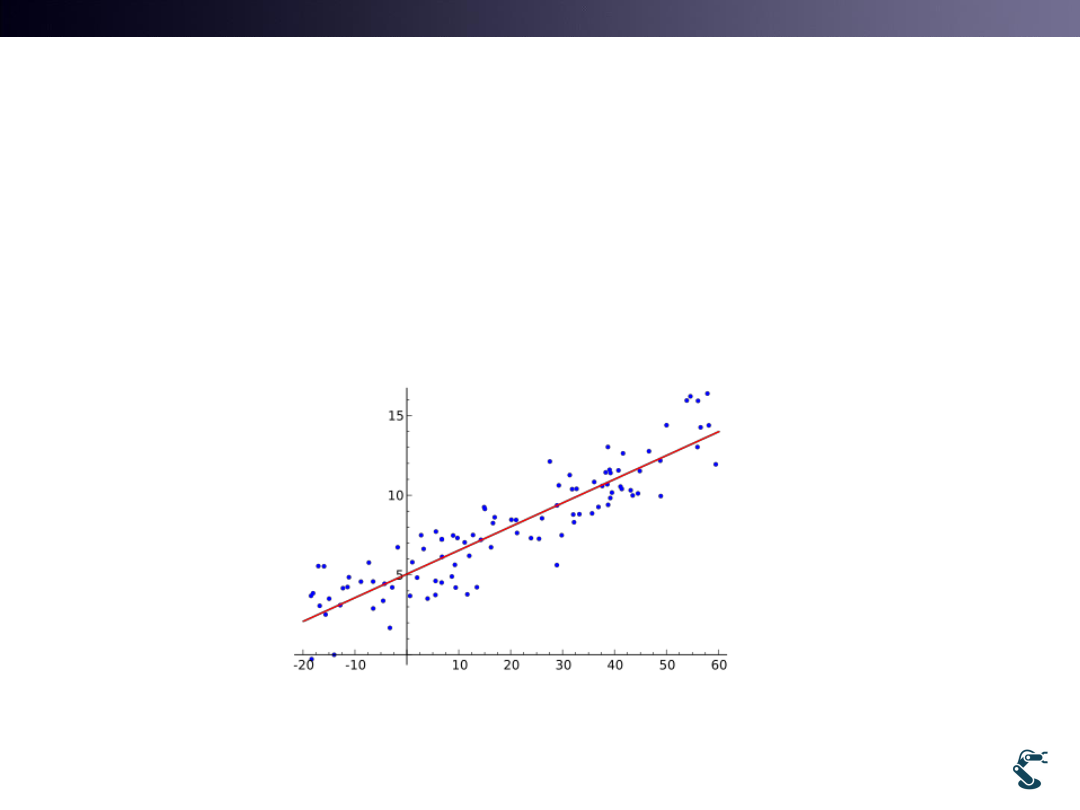
Regression
• The Most Important Issue in the field of Learnings.
• What is Regression?
– Simply, Curve fitting.
– Goal: find the best Curve or Line.
• In other words, Regression is in the filed of Optimization
3
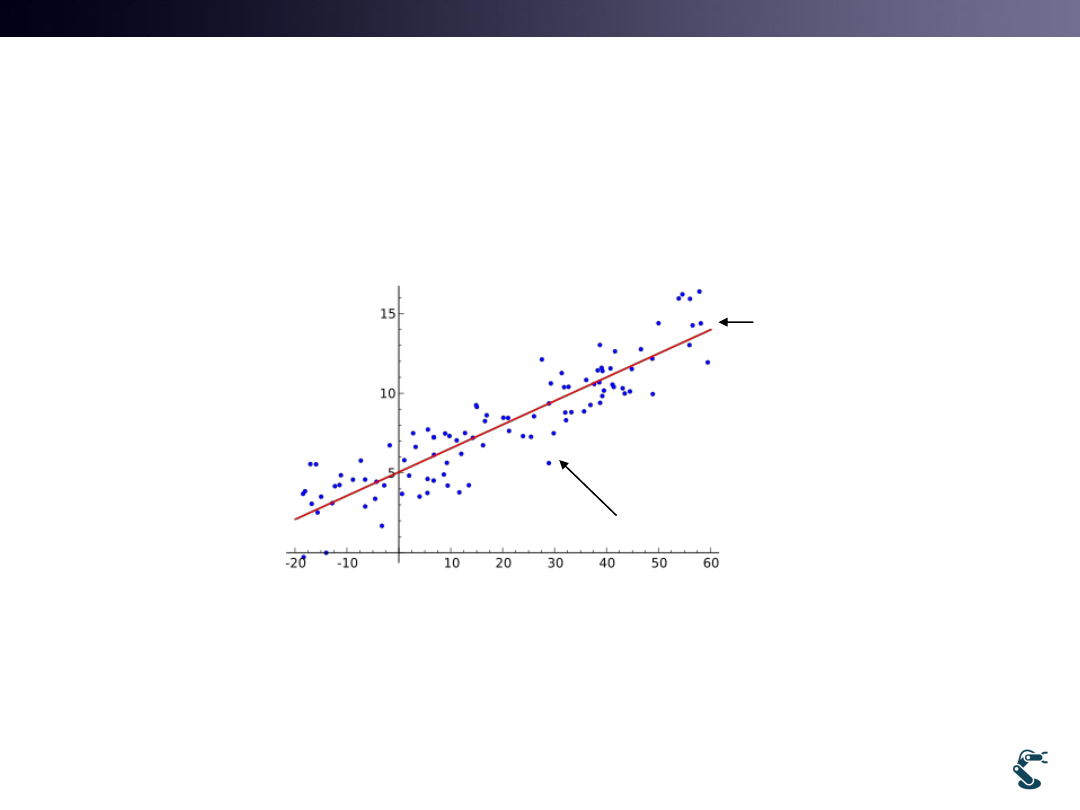
* Important
All samples CANNOT
satisfy the one Line!!!
It is an Optimal Problem
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
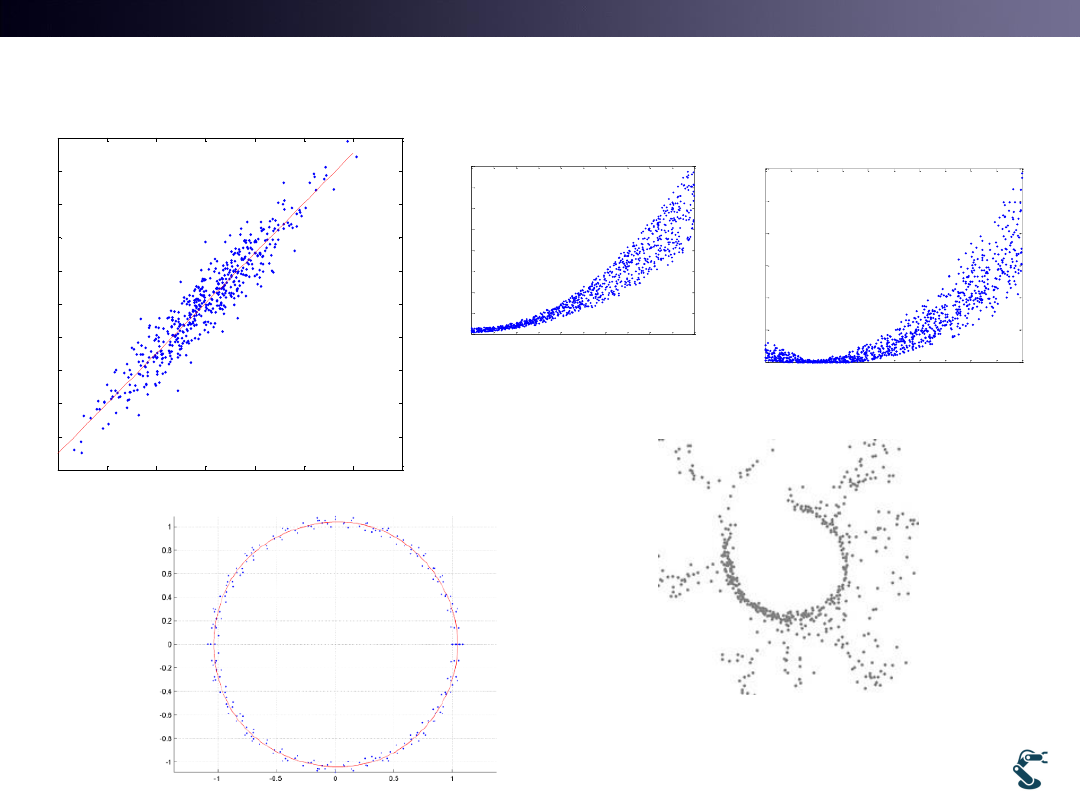
Regression Types
4
-1
0
1
2
3
4
5
6
-2
-1
0
1
2
3
4
5
6
7
8
Blue:Sample, Red:Estimated line
0
1
2
3
4
5
6
7
8
9
10
0
50
100
150
200
250
300
0
1
2
3
4
5
6
7
8
9
10
0
50
100
150
200
250
300
350
400
Linear
Linear
Non Linear
Non Linear
Non Linear
Stochastic
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Linear Regression
• Samples are given S={(x1,y1), (x2,y2),…, (xN,yN)}
• Goal: Find the a and b for minimizing Error
5
(xi, yi)
Red line:
y=ax+b
Knowns: (x1,y1),….(xN,yN)
Unknowns: a, b Our goal!!

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Linear Regression
Minimize Error Function
• Definition of J
– Error function or Cost function
• J is often the SUM of Squared Error (Least Square)
2
2
2
||
||
||
(
) ||
N
N
N
i
i
i
i
i
i
i
J
e
y
y
y
ax
b
2
Distance :
||
||
i
y
y
N=3
X1 = (x1,y1)=(1,2)
X2 = (x2,y2)=(2,3)
X3 = (x3,y3)=(2,2)
3
2
2
2
2
||
(
) ||
(2 (
))
(3 (2
))
(2 (2
))
( , )
i
i
i
J
y
ax
b
a b
a b
a b
J a b

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
How to Find the Minimum?
( in detailed ways later)
• 1. Differentiation
• 2. Iterative Method
– More than thousands of methods exist.
– Ex) Gradient Descent Method.
7
2
2
||
||
||
(
) ||
( , )
N
N
i
i
i
i
i
J
y
y
y
ax
b
J a b
When
0 and
0, J has minima or maxima.
J
J
a
b
Example)
2
(
1) , y'=2(x-1)=0
x=1 , y has minimum
y
x
when
1
n
n
x
x
J
Why we use Iterative Method in many applications
such as NN?

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Linear Regression Solution
8
2
2
||
||
||
(
) ||
( , )
N
N
i
i
i
i
i
J
y
y
y
ax
b
J a b
2
2
2
1
2
2
(
)
(
)
(
)
...
(
)
2(
)
(
)
2(
)(
)
(
)
2(
)(0
)
2(
)(0
)
2(
)(
)
0
N
i
i
N
N
N
i
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
i
i
i
y
y
y
y
y
y
a
a
y
y
y
y
y
y
y
y
y
y
a
a
a
a
ax
b
y
y
y
y
y
J
y
y
x
a
a
a
2
(
)
2(
)
(
)
(
)
2(
)(0
)
2(
)(0
)
2(
)( 1)
0
N
N
i
i
i
i
i
N
N
N
i
i
i
i
i
i
i
y
y
y
y
y
y
b
b
ax
b
y
y
y
y
y
y
y
J
b
b
b

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Linear Regression Solution
• Test 5.m
9
2(
)(
)
2(
)(
)
0
(1)
2(
)( 1)
0
1
(2)
1
N
N
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
i
i
i
N
i
i
i
N
N
N
i
i
i
i
i
N
N
N
i
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
y
y
x
y
ax
b
x
a
x x
b
x
x y
y
ax
b
a
x
b
y
x x
x
x y
a
b
x
y
Oops,
It is Linear!
Matrix calculation
is O.K.
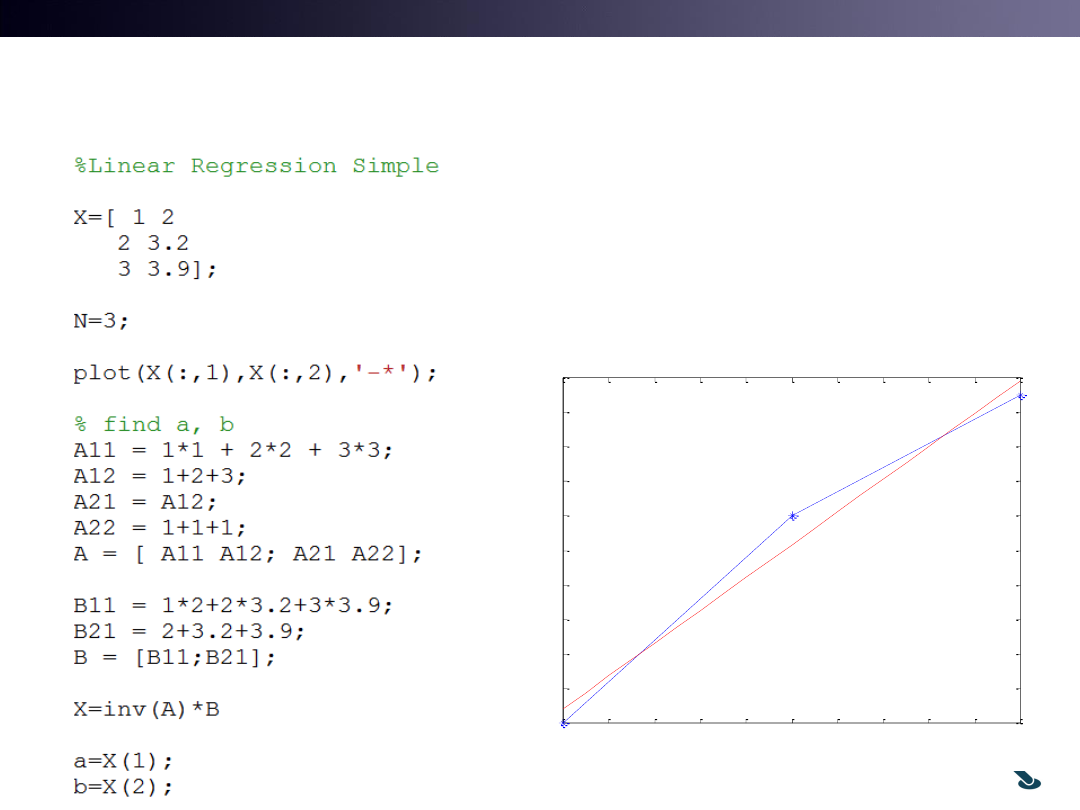
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Simple Example Test5.
10
1
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
3
2
2.2
2.4
2.6
2.8
3
3.2
3.4
3.6
3.8
4
Blue:Sample, Red:Estimated line
1
N
N
N
i
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
x x
x
x y
a
b
x
y
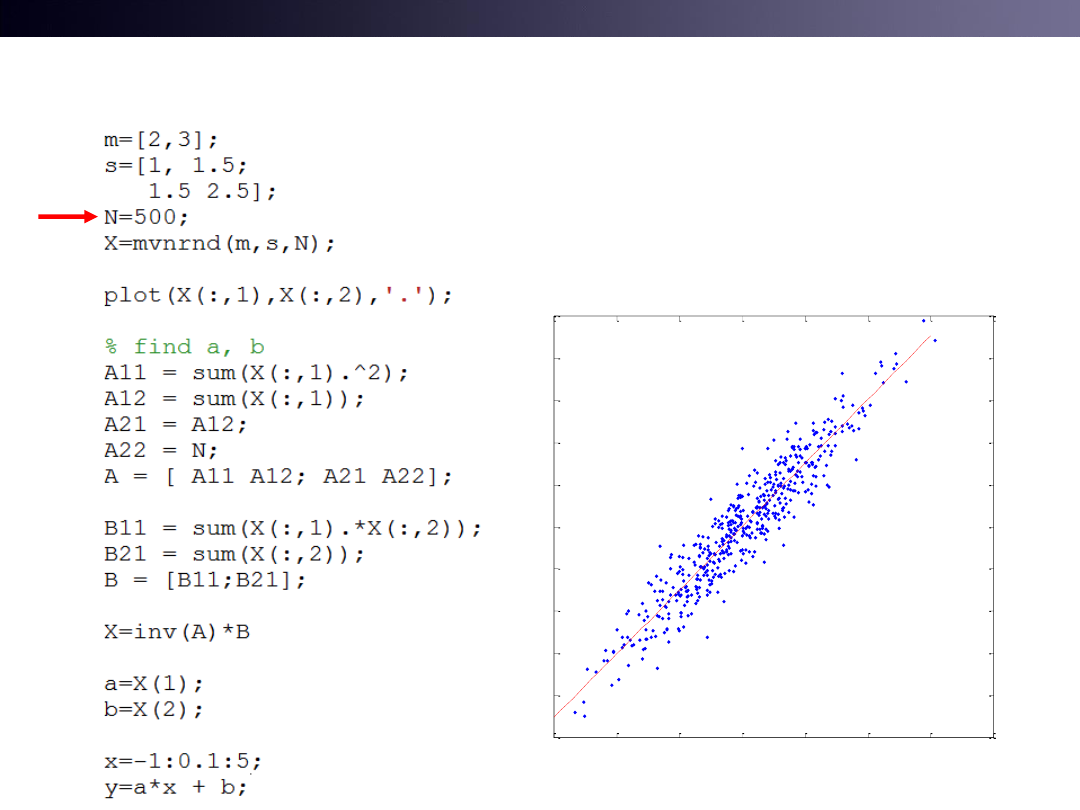
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Many Samples : Test6.m
11
-1
0
1
2
3
4
5
6
-2
-1
0
1
2
3
4
5
6
7
8
Blue:Sample, Red:Estimated line
1
N
N
N
i
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
x x
x
x y
a
b
x
y
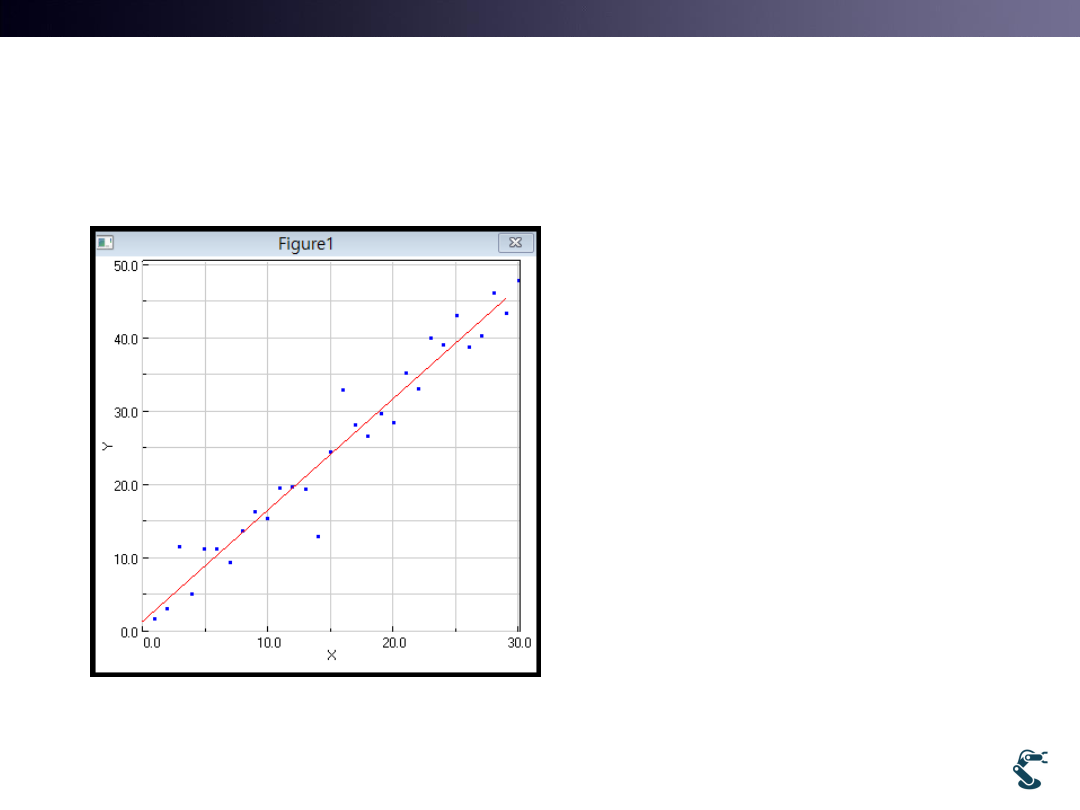
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Linear regression l2regline
ex/ml/l2regline
import l2regline
l2regline.test()
12
1
N
N
N
i
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
x x
x
x y
a
b
x
y
2
2
||
||
||
(
) ||
( , )
N
N
i
i
i
i
i
J
y
y
y
ax
b
J a b
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Question
• Regression works very well with Matrix Operation
• Well, How about the Curve?
13
How we
do fitting
with
Curves?
(or Linear algebra)
T&C LAB-AI
Regression( or Fitting Problem)
Non-Linear Problem
4
14
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
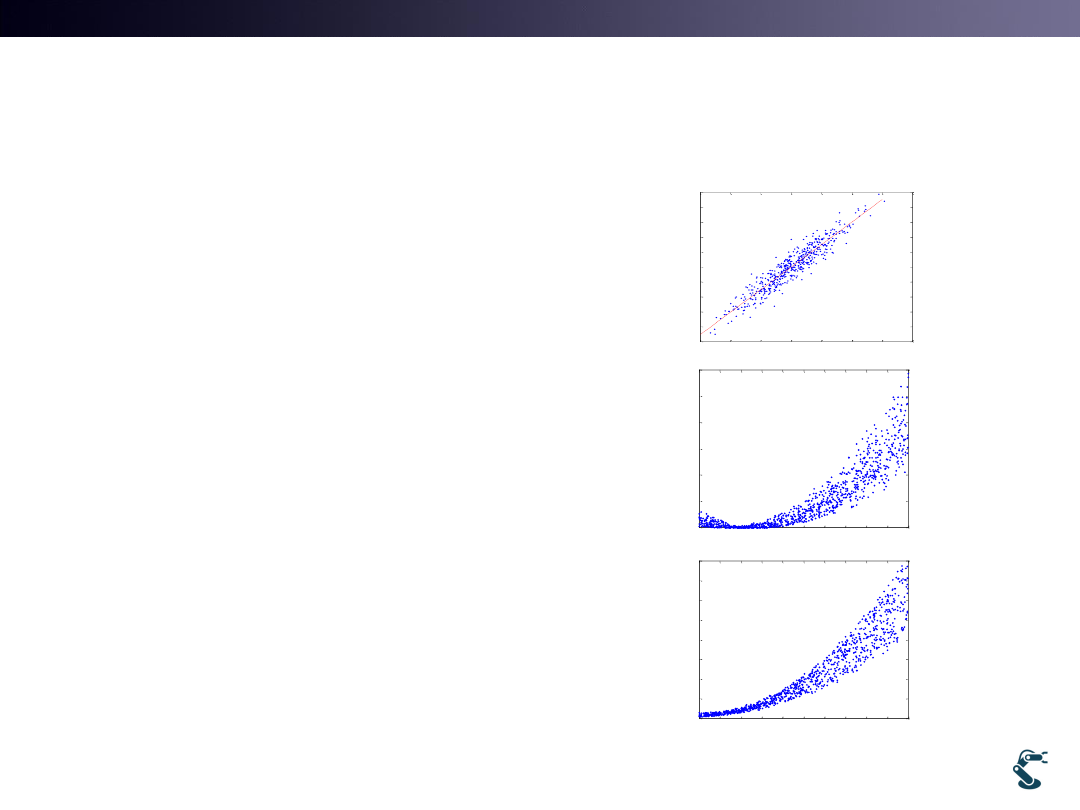
Question:
Curves are all Non Linear?
• Straight Line is Linear
• Some curves are Non Linear
• But, other curves are Linear.
• Let’s Answer
Which Curves are Nonlinear..
15
0
1
2
3
4
5
6
7
8
9
10
0
50
100
150
200
250
300
350
400
0
1
2
3
4
5
6
7
8
9
10
0
50
100
150
200
250
300
-1
0
1
2
3
4
5
6
-2
-1
0
1
2
3
4
5
6
7
8
Blue:Sample, Red:Estimated line
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
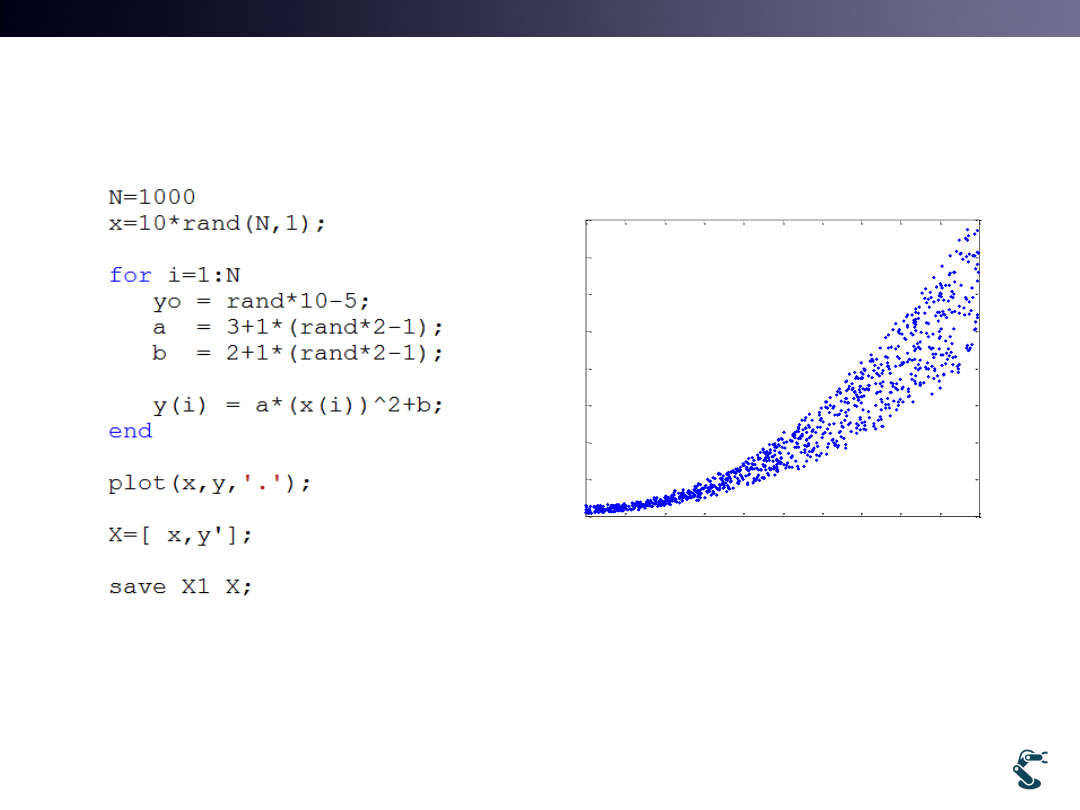
Regression with
16
2
y
ax
b
Generate data
with Gen1.m
0
1
2
3
4
5
6
7
8
9
10
0
50
100
150
200
250
300
350
400

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
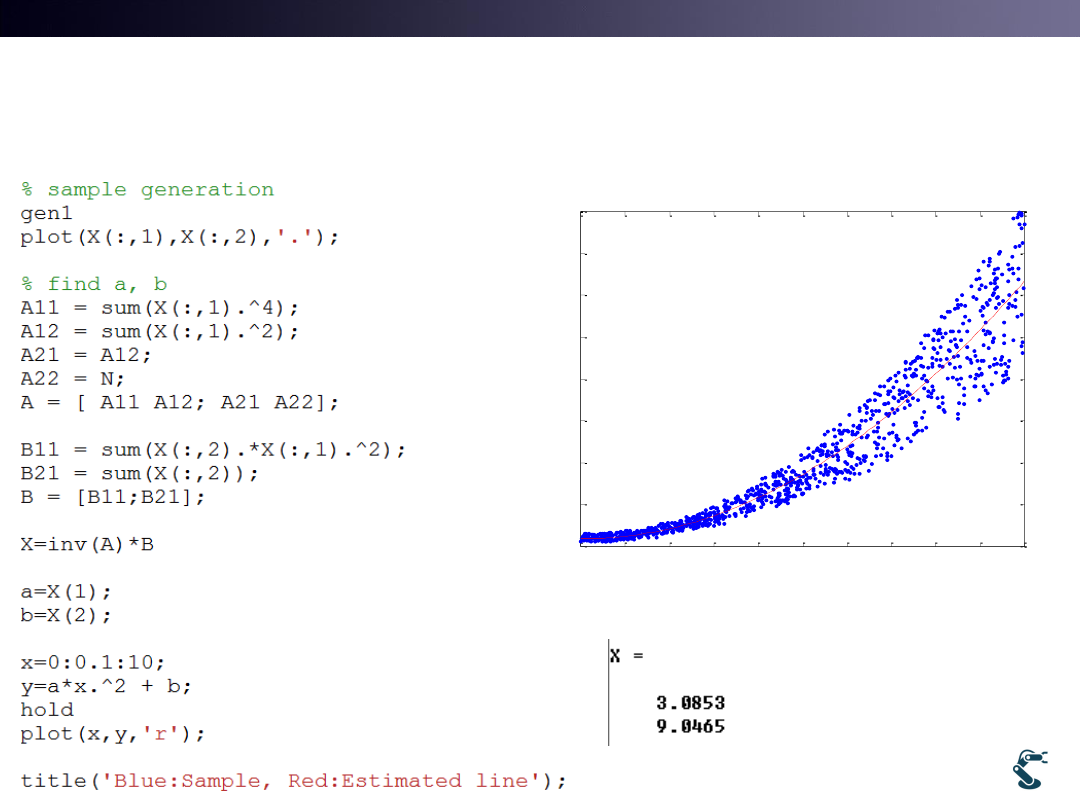
Regression Model
17
2
2
2
2
2
2
4
2
2
2
||
||
(
b)
2
(
b)(
)
0
2
(
b)( 1)
0
1
N
N
i
i
i
i
i
N
i
i
i
i
N
i
i
i
N
N
N
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
J
y
y
y
ax
J
y
ax
x
a
J
y
ax
b
a
x
b
x
y x
a
x
b
y
4
2
2
2
1
N
N
N
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
x
x
y x
a
b
x
y
Matrix Operation
is O.K.
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Test 7
18
0
1
2
3
4
5
6
7
8
9
10
0
50
100
150
200
250
300
350
400
Blue:Sample, Red:Estimated line
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
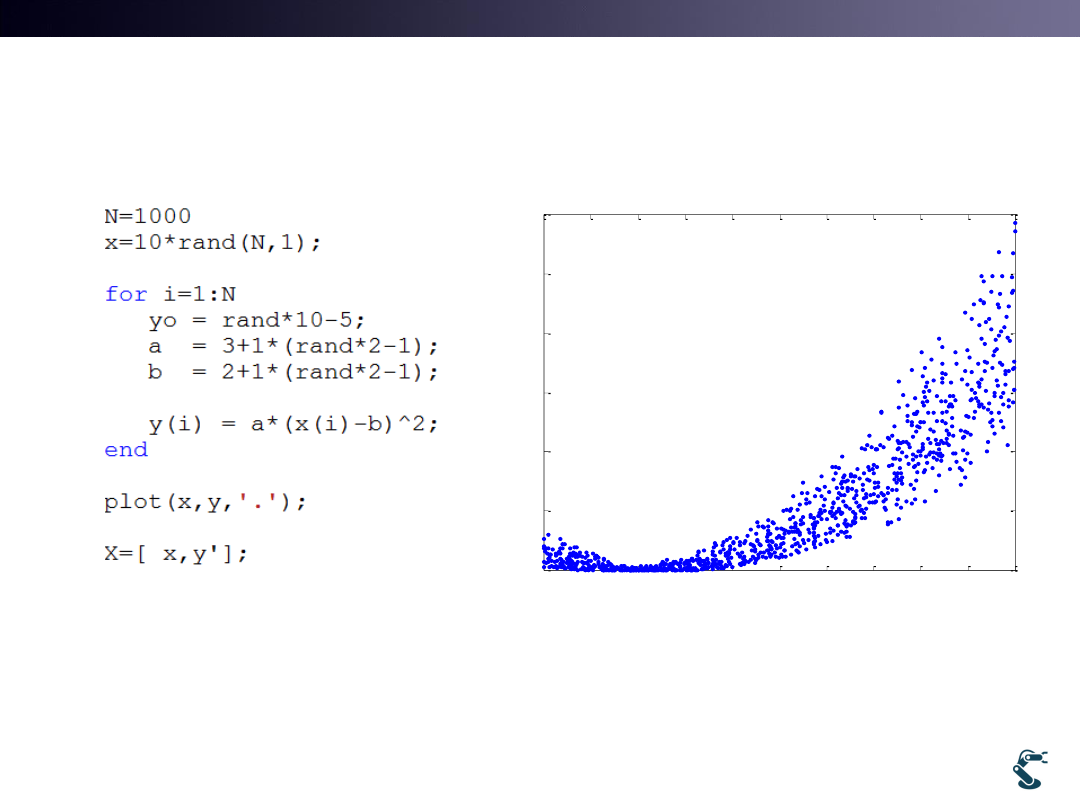
Regression with
19
2
(
)
y
a x b
0
1
2
3
4
5
6
7
8
9
10
0
50
100
150
200
250
300
Generate data
with Gen2.m

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Regression Model
20
2
2 2
2
2
2
||
||
(
(
) )
2
(
(
) )( (
) )
0
2
(
(
) )(2 (
))
0
N
N
i
i
i
i
i
N
i
i
i
i
N
i
i
i
i
J
y
y
y
a x
b
J
y
a x
b
x
b
a
J
y
a x
b
a x
b
b
2
2
2
(
(
) )( (
) )
( , )
0
(
(
) )(2 (
))
( , )
0
N
i
i
i
i
N
i
i
i
i
y
a x
b
x
b
f a b
y
a x
b
a x
b
g a b
Non Linear
Equation
N-R Eq

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Questions:
What is the Key Point?
That is Linear or Not.
• Don’t take it the wrong way owing to Curve types
• Linear Regression,
21
2
2
||
||
||
(
) ||
N
N
i
i
i
i
i
J
y
y
y
ax
b
2
2
2
||
||
(
b)
N
N
i
i
i
i
i
J
y
y
y
ax
1
N
N
N
i
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
x x
x
x y
a
b
x
y
4
2
2
2
1
N
N
N
i
i
i
i
i
i
i
N
N
N
i
i
i
i
i
x
x
y x
a
b
x
y
y
ax b
2
y
ax
b
2
()
y
ax
b
a
b
Linear

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Definition of Linearity
• Scalar Multiplication
• Additivity
* Remind that
22
,
if v
L it also satisfies
v
L
1
2
1
2
and
,
if v
L
v
L
then it also satisfies
v
v
L
2
(
)
([]
)
[]
It is NOT Linear!
y
a x b
a
b
a
ab

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Back To pp.19
This Regression has Nonlinear Equations
• How to solve it?
1.
23
2
2
2
(
(
) )( (
) )
( , )
0
(
(
) )(2 (
))
( , )
0
N
i
i
i
i
N
i
i
i
i
y
a x
b
x
b
f a b
y
a x
b
a x
b
g a b
2
||
||
( , )
0,
( , )
0
N
i
i
J
y
y
J
J
f a b
g a b
a
b
Nonlinear Newton-
Raphson in pp. 19
1
1
1
ˆ
ˆ
ˆ
(
)
0
( )
ˆ
ˆ
ˆ
ˆ
ˆ
k
k
k
F x
h
F x
Jh
h
J F
x
x
h
x
J F
2
(
)
y
a x b

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
• How to solve it?
2. Optimization
For example, Gradient Descent Method (GDM)
24
2
2 2
1
||
||
(
(
) )
N
N
i
i
i
i
i
n
n
J
y
y
y
a x
b
a
w
b
w
w
J
2
2 2
2
2
2
||
||
(
(
) )
i
j
2
(
(
) )( (
) ) i
2
(
(
) )(2 (
)) j
N
N
i
i
i
i
i
N
N
i
i
i
i
i
i
i
i
J
y
y
y
a x
b
J
J
J
a
b
y
a x
b
x
b
y
a x
b
a x
b

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
How to Find the Minimum?
• 1. Differentiation (Linear Equation)
• 2. Iterative Method (Non-Linear Equation)
– More than thousands of methods exist.
– Ex) Gradient Descent Method.
25
2
2
1
2
3
||
||
||
(
) ||
( , )
(
,
,
,....
)
N
N
i
i
i
i
i
N
J
y
y
y
ax
b
J a b
J
J w w w
w
1
2
3
0,
0,
0,...
0
,
N
J
J
J
J
w
w
w
w
if it is linear eqs then Aw
b
1
n
n
x
x
J