
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Robot Learning
2. Numerical Method
Jeong-Yean Yang
2020/10/22
1

T&C LAB-AI
Numerical Method
1. Equation Solver
2. Multiple Nonlinear Equation
3. Linear Regression
4. Nonlinear Regression
5. Stochastic Regression (RANSAC)
6. Optimization
0
2
T&C LAB-AI
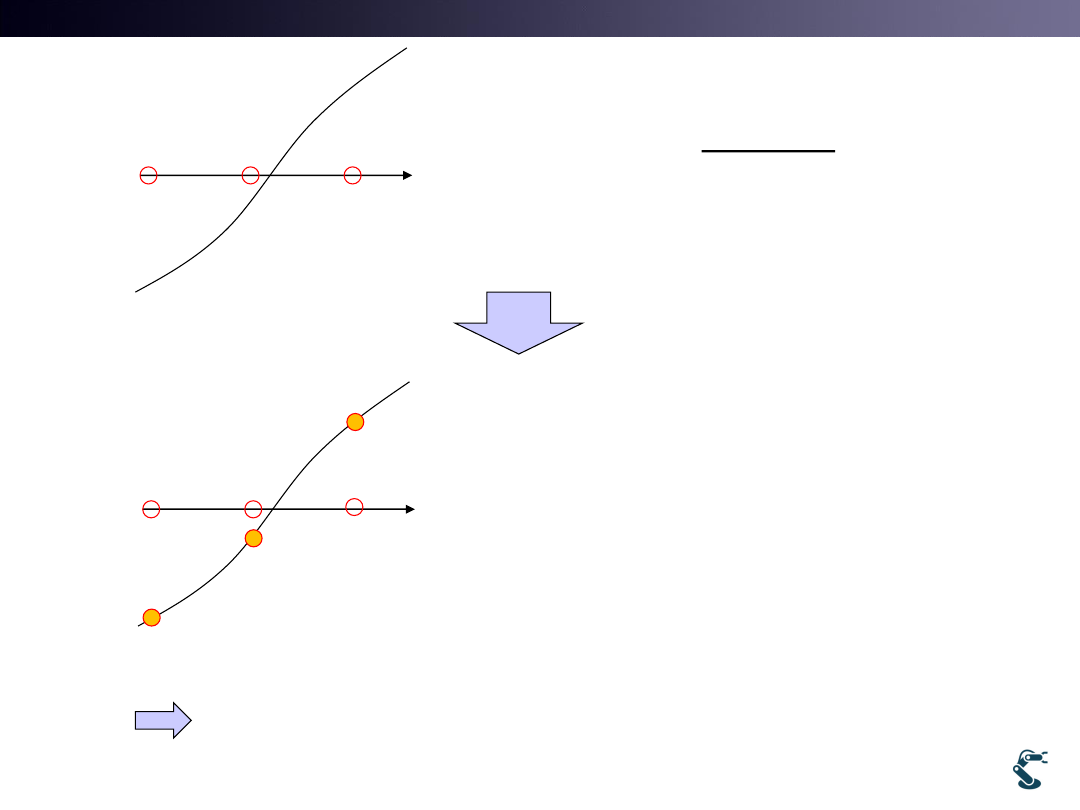
Deterministic Vs. Stochastic Method
First Start with Numerical Methods
1
3

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Deterministic Vs. Stochastic World
• Deterministic World
– Everything must be determined.
– Everything is Understood by Modeling
– Manipulator-based Robotics, PID or even Robust Control
– Pseudo code :
• Stochastic World
– Everything is PROBABILISTICALLY determined
– Every phenomenon occurs by Probabilistic Results
– Autonomous locomotion(SLAM), Learning, and so on
– Pseudo code:
4
2
2
1
1
3
(3,
)
exp
2
2
x
a
N
3
a
Equality “=“ is
NOT allowed.
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Why we learn first Deterministic Method?
• Some methods look like Non-Deterministic Problem.
• Fitting, Regression, Control
• Ex) Control tries to be in the desired goal in spite of
unnecessary system dynamics, Is it probabilistic?
• Absolutely, Not.
5
Regression
Curve fitting
Control

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Many Deterministic Methods are based
on Mathematical Model
• Controller is well designed to OVERCOME marginal
error Deterministic method
• Fitting or Regression is to Minimize Errors
Deterministic Method
• Then, What is Stochastic Process?
– Probabilistically, next state is determined.
• 1.Many Deterministic Methods are applied to
Learning Methods
• 2. We learn the differences of
Deterministic and Stochastic Methods.
6

T&C LAB-AI
Numerical Methods for
Solving Equation, f(x)=0
2
7

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Numerical Method:
The goal is to find the solution
• Analytical Solution
• Numerical Solution( or Computational Solution)
• Solve 2a=3 equation by using computer program
8
2
3
1.5
a
a
: 2
3
: ( )
2
3
Equation
a
Function f a
a
( )
2
3
0 ?
How to find f a
a
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Numerical Method
Solve Equation(or Finding Roots)
• Solve Equation
– Equation: f(x,y,s,t) = 0
• How to solve it by Numerical Method?
• Iteratively, find a solution by a Computer
9
Iteration

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Why Numerical Methods are Required?
• 1. Equations are Complex
– Remind Robot Kinematics or Dynamics are very complex
– Generally, we CANNOT solve it by analytical methods
• 2. We learn Convergence by Iterative Methods
– Iteration: In Each turn, a method moves to the solution
– Convergence or Divergence Problem
– Dynamic Programming: Learning, Control, Numerical
Methods, etc.
10
2
2
2
2
1 1
2 1
2 2
2 1 2 2
2 2
2 1 2 2
1
2
2
2 2
2 1 2 2
2 2
2
1 1 1
2
2 12
1 1
2 1 2
1
2
2
2
2
2 2 12
2 1 2 1
2
2
(
)
(2
)
m l
m l
m l
m l l c
m l
m l l c
m l
m l l c
m l
m l c
m l c
l c
m l l
s
g
m l c
m l l
s
0
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
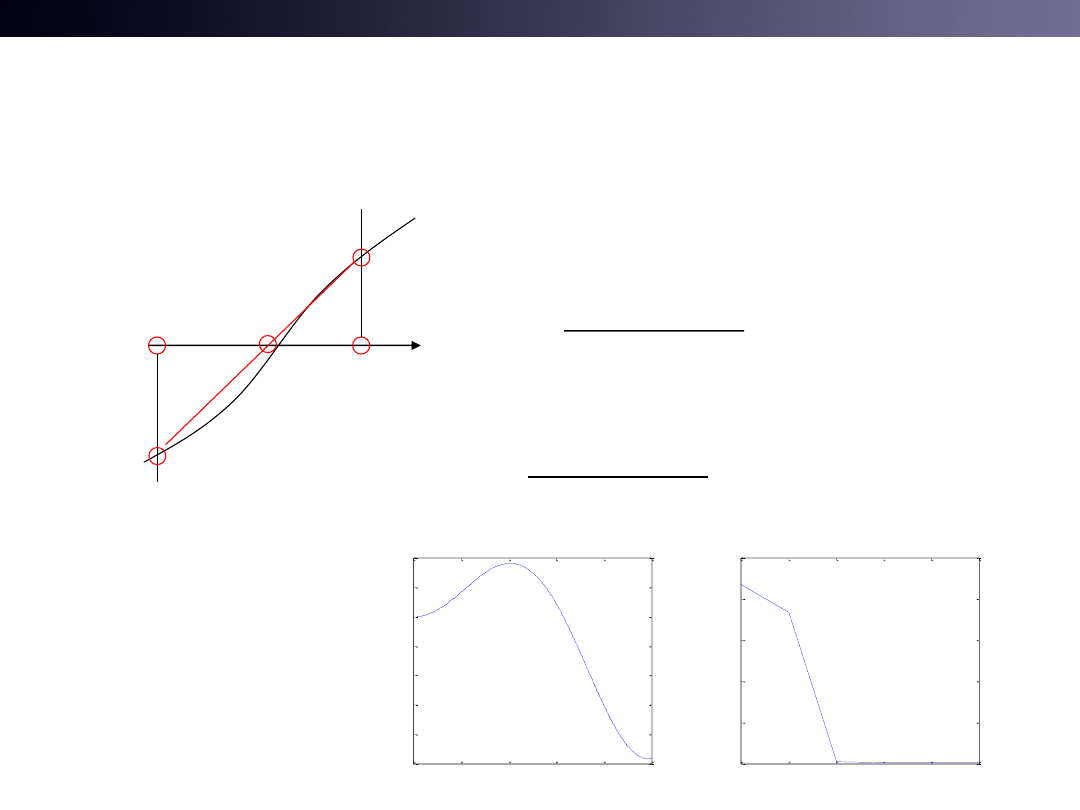
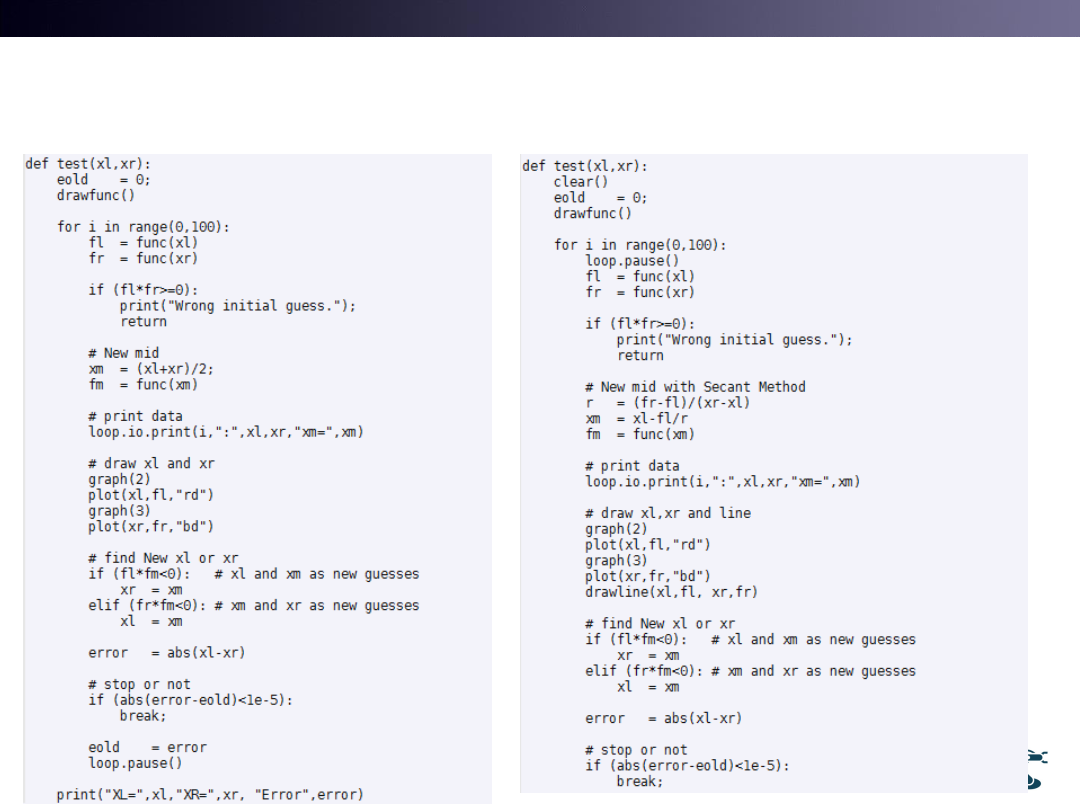
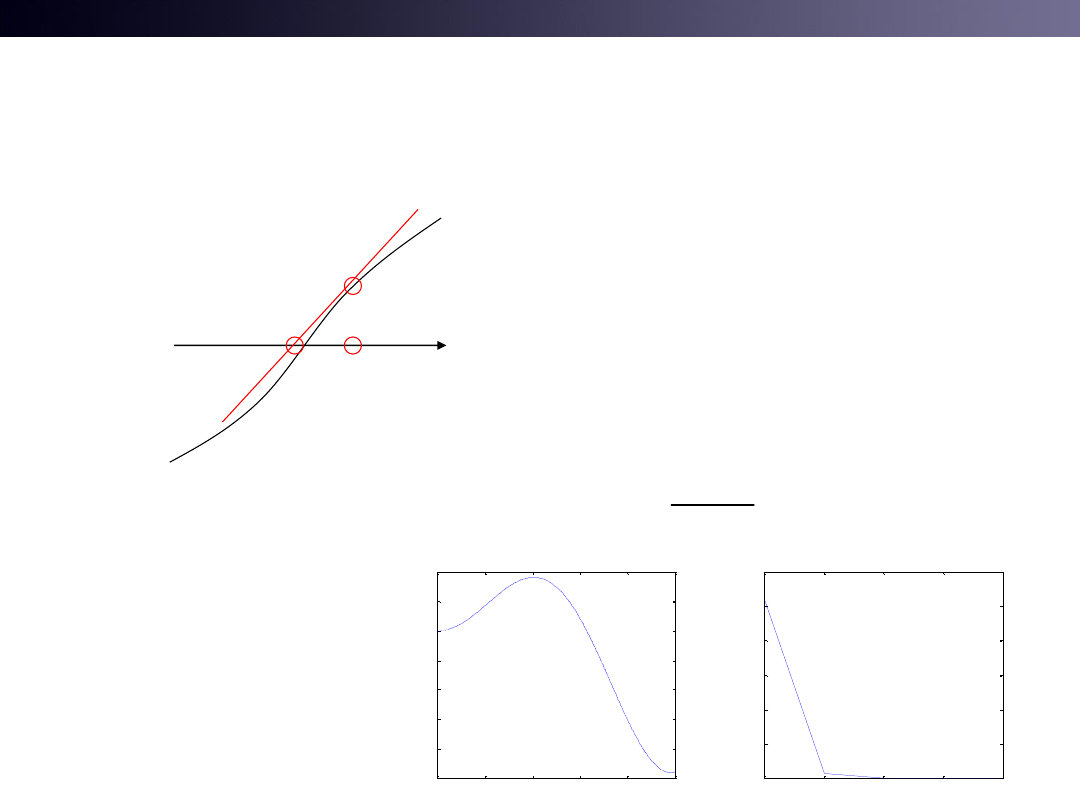
Numerical Method: 1.
Bisection Method
11
Algorithm
1. Start with two points
Assume
2. Find mid point
L
s
R
x
x
x
2
L
R
m
x
x
x
( )
f x
(
) (
)
0
L
R
f x
f x
(
) (
)
0 :
'
(
) (
)
0 :
'
m
L
m
R
m
R
m
L
f x
f x
x
x
f x
f x
x
x
sin
0
x
x
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
x
y
xsin(x)
0
5
10
15
20
0
0.5
1
1.5
iteration
|e
|
• See test1.m
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
12
L
x
R
x
1st turn
2
L
R
m
x
x
x
m
x
Question: Xm is left or Right?
L
x
R
x
m
x
(
)
L
f x
(
)
m
f x
(
)
R
f x
(
) (
)
0
L
R
f x
f x
Solution, X is always between
XL<X<XR
Thus, Xm will be left or right
(
) (
)
0, new
(
) (
)
0, new
L
m
R
m
R
m
L
m
if f x
f x
x
x
if f x
f x
x
x
L
m
x
x
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Convergence
• Modeling it as you have Learned in other classes
13
2
L
R
m
x
x
x
1
x
2
x
3
x
4
x
5
x
1
2
3
4
,
,
,
,.....
n
x x x x
x
1
2
1
2
3
2
| e | |
|
| e | |
|
...
x
x
x
x
2
1
3
2
|
|
|
|
2
x
x
x
x
1
1
2
2
1
1
1
2
1
2
1
1
1
|
|
|
|
|
|
|
| |
|
...
2
4
2
|
|
1
lim |
| lim
|
| lim
0
2
2
lim |
| 0
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
x
x
x
x
x
x
e
x
x
x
x
e
x
x
e
| e | |
|
L
R
x
x

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Bisection Method is Too Slow
14
1/2
1/2
1/2
• If the initial XL or XR is too far from a solution, ½ is
NOT so Fast!
• How can we speed up?
– Ratio of a Function is better than 1/2 .
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Numerical Method: 2.Secant Method
• See test2.m
15
( )
f x
Algorithm
1. Start with two points
2. Find mid point
(
)
(
)
(
)
(
)
0
R
L
L
L
R
L
f x
f x
y
x
x
f x
x
x
L
x
R
x
(
)
(
)
(
)
(
)
0
R
L
m
L
L
R
L
f x
f x
x
x
f x
x
x
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
x
y
xsin(x)
1
2
3
4
5
6
0
0.5
1
1.5
2
2.5
iteration
|e
|
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Why Secant Method is Faster than
Bisection Method?
• Focus on a new Mid point.
• Function Ratio is good for faster convergence.
• What does the Function Ratio remind us of?
16
(
)
(
)
(
)
(
)
0
R
L
L
L
R
L
f x
f x
y
x
x
f x
x
x
Differentiation!
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
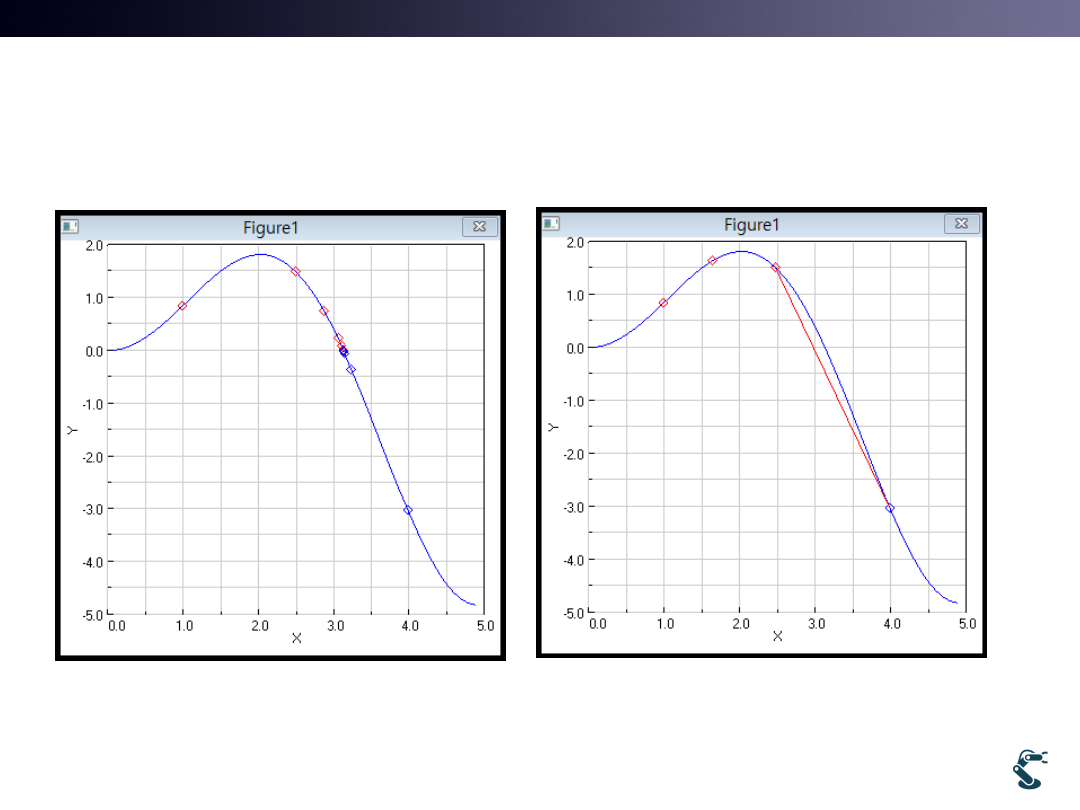
Example) l2bisect and l2secant
ex/ml/l2bisect and ex/ml/l2secant
17
import l2bisect
l2bisect.test(1,4)
import l2secant
l2secant.test(1,4)
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
ex/ml/l2bisect and ex/ml/l2secant
18
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
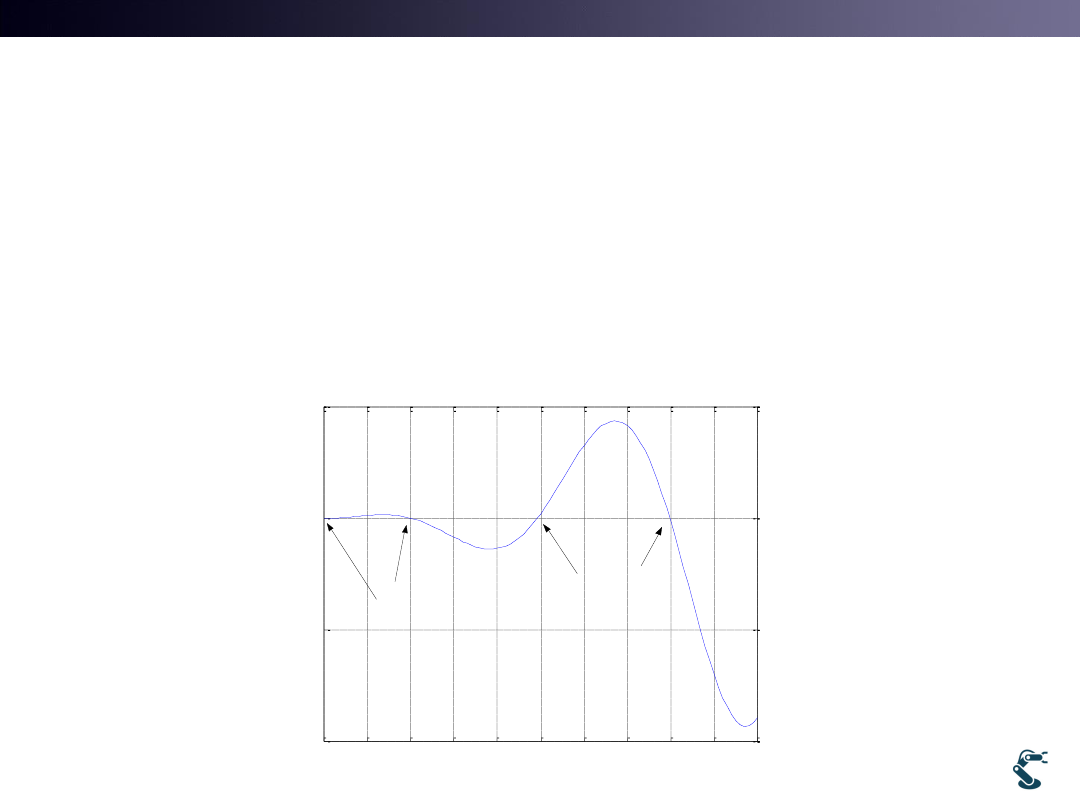
HW1) Find the Solution X
with Bisection and Secant Methods
• Given Equation x*sin(x)+x^2*cos(x)=0
• Condition 0<x<10
• Find all solution, x within the range [0,10]
19
0
1
2
3
4
5
6
7
8
9
10
-100
-50
0
50
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Numerical Method:
3. Newton-Raphson (NR) Method
• See test3.m
20
( )
f x
Algorithm
1. Start with one point( a GUESS value)
2. Find a new point
'(
)(
)
(
)
0
n
n
n
y
f x
x
x
f x
1
1
'(
)(
)
(
)
0
(
)
'(
)
n
n
n
n
n
n
n
n
f x
x
x
f x
f x
x
x
f x
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
x
y
xsin(x)
1
2
3
4
5
0
2
4
6
8
10
12
iteration
|e
|
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
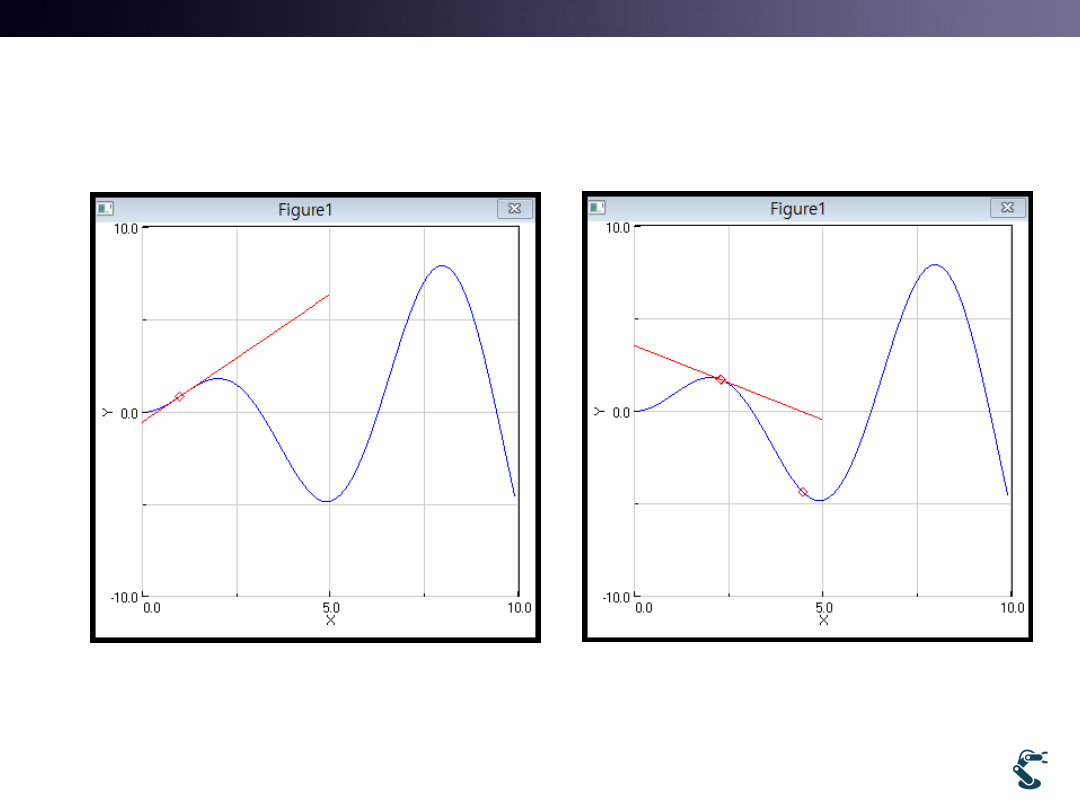
Example) Newton-Raphson
ex/ml/l2nr
21
import l2nr
l2nr.test(0.1)
import l2nr
l2nr.test(2.3)

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Comparison Three Cases
22
2
L
R
m
x
x
x
1
(
)
'(
)
n
n
n
n
f x
x
x
f x
(
)
(
)
(
)
L
m
L
R
L
R
L
f x
x
x
f x
f x
x
x
Bisection
Secant
Newton-Raphson
2
4
6
8
10
12
14
16
18
20
0
0.5
1
1.5
2
2.5
3
iteration
|e
|
2
4
6
8
10
12
14
16
18
20
0
0.5
1
1.5
2
2.5
3
iteration
|e
|
2
4
6
8
10
12
14
16
18
20
0
0.5
1
1.5
2
2.5
3
iteration
|e
|
Exponentially Converged
Good for convergence:
-Stable
-Continuous and smooth
convergence but Slow
Using Ratio = Linearization
Many Nonlinear problems
are approximated for
linearity.
Using Ratio = Linearized
method with Differentiation
- Fast
- But, initial guess is
important for stability

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Solution Analysis
• Bisection Method
– Is it Bad?
– Exponentially Converged Stable
• Secant Method(Faster)
• NR Method(much Faster)
– Sometimes, it becomes very unstable.
23
|
| 2
k
n
e
(
)
(
)
(
)
L
m
L
R
L
R
L
f x
x
x
f x
f x
x
x
(
)
(
)
0,
.
R
L
R
L
f x
f x
if
it fails
x
x
1
(
)
'(
)
n
n
n
n
f x
x
x
f x
'(
)
0,
.
n
if f x
it fails
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
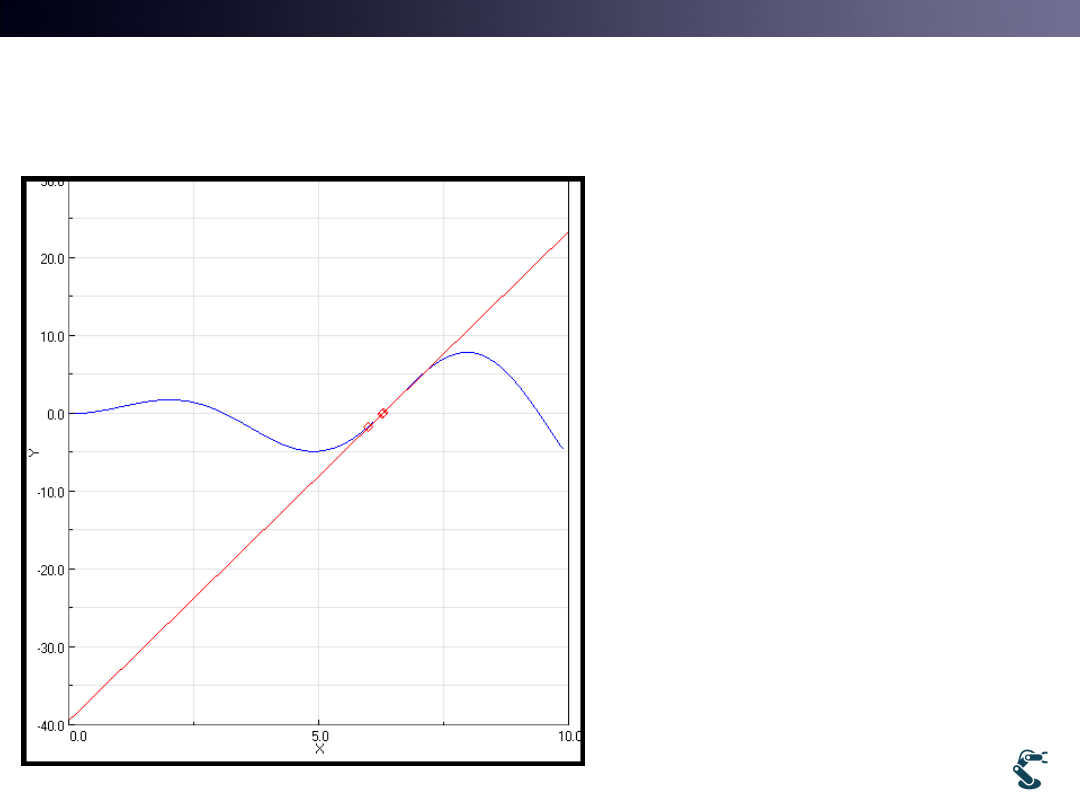
HW2)N-R method
How we get solution x= 6.28318?
• Hint: Change your
initial guess
24
T&C LAB-AI
Numerical Methods for
Multiple Equations
f(x,y)=0 and g(x,y)=0
3
25
2
2
2
2
1 1
2 1
2 2
2 1 2 2
2 2
2 1 2 2
1
2
2
2 2
2 1 2 2
2 2
2
1 1 1
2
2 12
1 1
2 1 2
1
2
2 2
2
2 2 12
2 1 2 1
2
2
(
)
(2
)
m l
m l
m l
m l l c
m l
m l l c
m l
m l l c
m l
m l c
m l c
l c
m l l
s
g
m l c
m l l
s
0
1
2
1
2
1
2
1
2
1
2
1
2
( ,
, ,
, ,
)
0
g( ,
, ,
, ,
)
0
f

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Multi Dimension Equation
• 1 Dim. Problem
– Solve x with f(x)=0
• 2 Dim. Problem
– Solve vector x
26
1
(
)
, Iteration
'(
)
n
n
n
n
f x
x
x
f x
n
s
x
x
( , )
0
( , )
0
f x y
g x y
2
2
( , )
3
0
( , )
1
0
f x y
x
y
g x y
x
y
Ex)
1
1
1
1
( , y)
ˆ
,
( , )
(
)
ˆ
ˆ
ˆ
, Iteration
'(
)
n
n
n
n
n
n
n
s
n
x
f x
X
F
y
g x y
F x
X
X
X
X
F x
Matrix and Vector

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Multi Dim. NR uses Matrix
27
1
1
1
1
( , y)
(
)
ˆ
ˆ
ˆ
,
( , )
'(
)
n
n
n
n
n
n
n
x
f x
F x
X
F
X
X
y
g x
F x
y
Matrix has NO DIVISION.
'(
)(
)
(
)
0
n
n
n
y
f x
x
x
f x
1
1
'(
)(
)
(
)
0
(
)
'(
)
n
n
n
n
n
n
n
n
f x
x
x
f x
f x
x
x
f x
1
1
1
1
1
1
1
ˆ ˆ
ˆ
ˆ
'(
)
0
ˆ ˆ
ˆ
ˆ
'(
)
ˆ
ˆ
ˆ
ˆ
'
ˆ
ˆ
ˆ
ˆ
'
ˆ
ˆ
n
n
n
n
n
n
n
n
n
F X
X
F
F X
X
F
X
X
F
F
X
X
F
F
X
J F
Jacobian Matrix
J
Remind that Multi Dim. NR requires,
- Matrix calculation
- Differentiation Jacobian Matrix
- Division Inverse matrix

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Another Derivation:
NR Method for Non-Linear Equations
• Non linear Equations, f(x,y)=0 , g(x,y)=0
– Solve x,y
• Define F(x,y)
• Taylor series( or Differentiation)
• Remind F(x,y)=0
28
( , )
( , )
( , )
f x y
F x y
g x y
ˆ
ˆ
ˆ
ˆ
(
)
( )
( )
ˆ
ˆ
ˆ
(
)
( )
i
i
i
j
i
i
j
j
F
F x
h
F x
h
F x
J h
x
F x
h
F x
Jh
1
1
1
ˆ
ˆ
ˆ
(
)
0
( )
ˆ
ˆ
ˆ
ˆ
ˆ
k
k
k
F x
h
F x
Jh
h
J F
x
x
h
x
J F
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Example) nlnr.m
• X0=3, y0=1
29
2
2
10
5
f
x
y
g
xy
2
2
( , g)
( , )
f
f
x
y
x
y
f
J
g
g
y
x
x y
x
y
1
1
1
ˆ
ˆ
'
ˆ
ˆ
'
f
h
J F
J
g
x
x
x
f
X
h
J
y
y
y
g
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
Non-Linear Newtown-Raphson Method
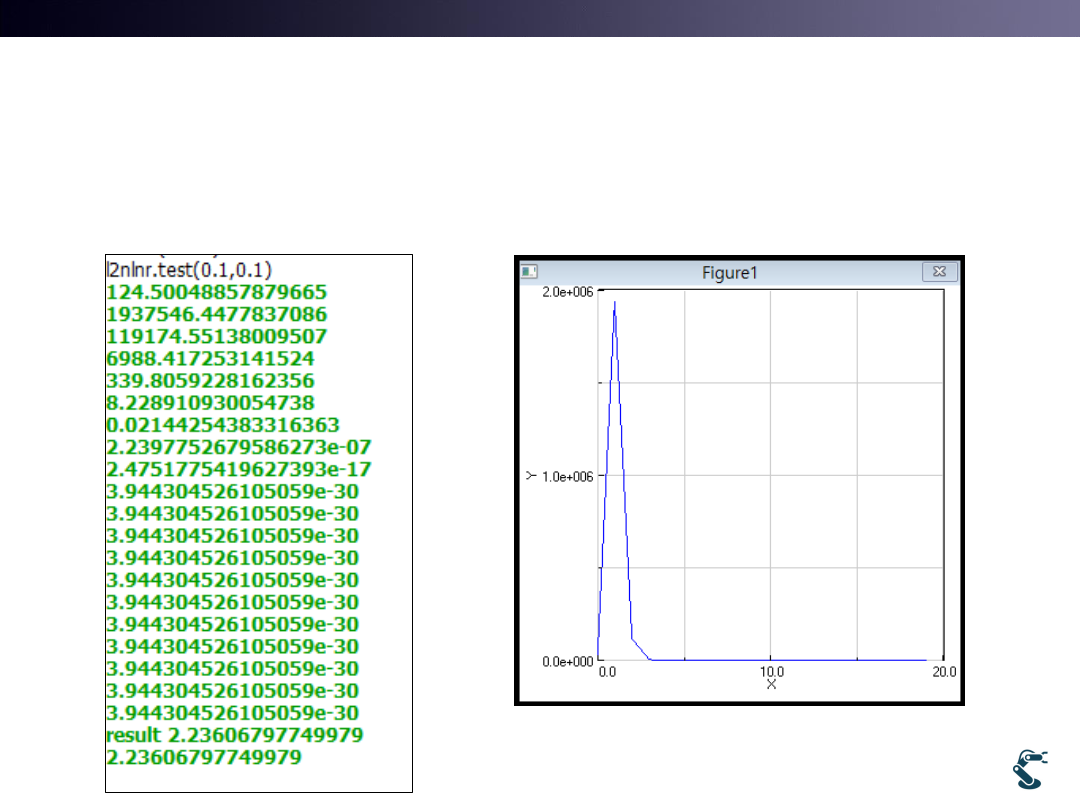
• See l2nlnr
30
Error becomes 3.9 e-30

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
2DOF SCARA Robot Inverse Kinematics Solver
with Nonlinear NR Method
ex/ml/l2nrscara
• Forward Kinematics( See Robotics Lecture4, pp.20)
• When x,y are given,
– X = 8.1603
– Y= 5.7139
• Question: What are q1, q2 ?
• Solve it with Nonlinear Newton Raphson Method
31
1
1
2
1
2
1
1
2
1
2
cos( )
cos(
)
sin( )
sin(
)
x
l
l
y
l
l
L1 = L2= 5
HW 3
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
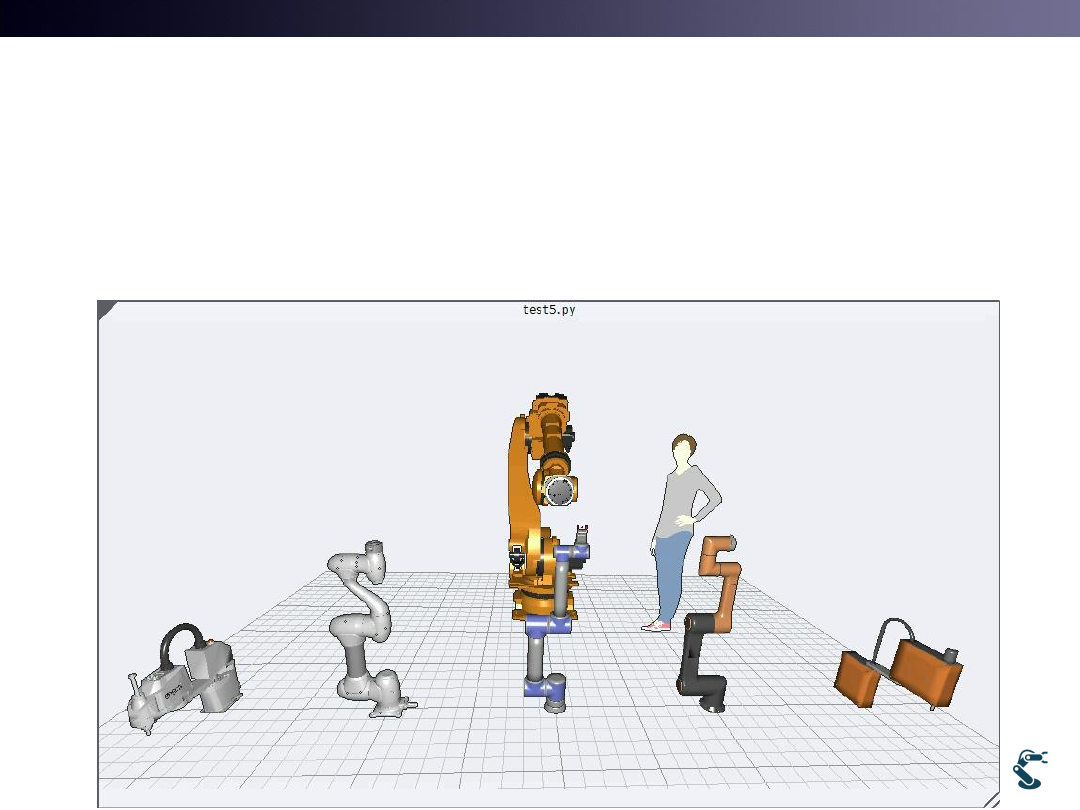
Inverse Kinematics in Robotics
• In recent years, Most robots solve IK with Nonlinear
Newtown-Raphson Method
32
T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
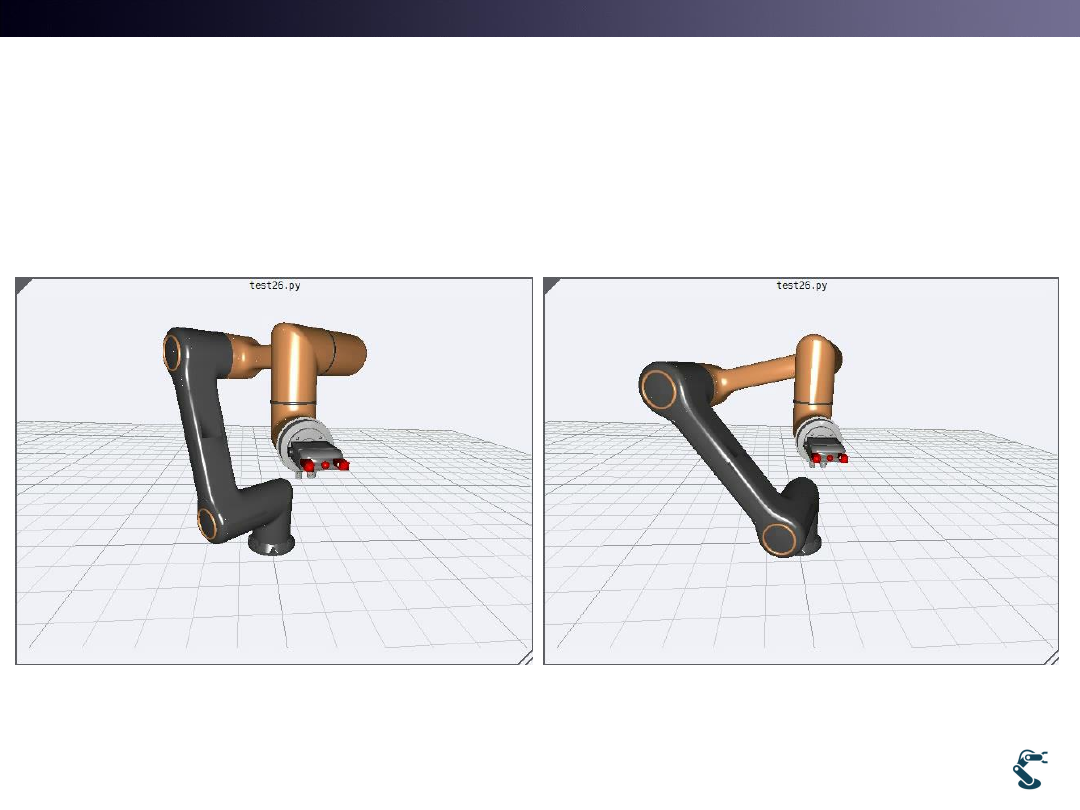
Many Cooperative Robots do NOT have
Analytical Inverse Kinematics
Nonlinear Newton-Raphson Method
(or Inverse Jacobian Method)
33

T&C LAB-AI
Dept. of Intelligent Robot Eng. MU
Robotics
34